基于彈性聯軸環節的行波型超聲波電動機瞬態特性
周廣睿,郭吉豐,傅平,丁敬,王光慶
(浙江大學,浙江杭卅I 310027)
摘要:計及了聯軸節等環節的彈性和定轉子力傳遞模型,建立了描述瞬態特性的運動微分方程,并給出其解。利用超聲波瞬態特性測試系統,理淪和實驗驗證了上述模型的準確陛和有效眭,并鶯點指出r影響響應時間的阻尼系數主要來源于接觸面的摩擦阻尼,而非電機轉軸上摩擦阻尼。
關鍵詞:行波型超聲波電動機;彈性聯軸節;瞬態特性
中圈分類號:TM35 文獻標識碼:A 文章編號:1004—7018(2008)01—0017一04
引 言
超聲波電動機是通過高頻振動和摩擦驅動的電機,具有結構簡單、響應速度快、斷電自鎖、低速大轉矩等特點,而低速大轉矩等特性在許多設備中已經得到充分應用。超聲波電動機的高分辨率和步進特性與其響應速度快有關,因此對其瞬態特性的研究不僅有助于對超聲波電動機的認識,電有助于更好地應用這一特點。
目前,分析超聲波電動機的瞬態特性時有兩個特點。一是通常忽略聯軸節和電機軸等連接環節的彈性,采用剛性連接的模型來建立動力學方程[1-5],這對電機運行的穩態特性分析影響不大,但對電機起動或者斷電自鎖時瞬態過程的特性分析的影響卻非常突出。這樣的模型與實際用光電編碼器連接的測試系統有一定的出入。二是以往的分析對電機軸的阻尼系數常采用辨識等方法,缺乏其產生原因和主要影響因素的定量分析。基于上述兩點,本文引
入彈性聯軸節模型和定轉子摩擦驅動力傳遞模型,建立了相應的微分方程,并給出解析解。同時通過測試系統實現了超聲波電動機的瞬態特性測試,從理論和實驗兩方面分析了瞬態特性。
1瞬態特性的理論分析
1.1問題簡化和力學模型
超聲波電動機起動和關斷的瞬態過程均包括兩個階段。在起動過程的第一個階段,定子表面行波振幅從起動瞬間的零振幅增加至穩態振幅,轉子處于一個較低的轉速;第二個階段,轉子加速直至穩態轉速,起動完成。同樣,在關斷過程的第一個階段,定子表面行波振幅從關斷瞬間的穩態振幅衰減為零,行波消失,轉子開始減速;第二個階段,轉子繼續減速至轉速為零,電機關斷。
起動和關斷過程的第一個階段均為定子行波變化的階段。一般來說,在分析瞬態特性時,可以忽略這一個階段,而認為定子表面行波的變化為階躍響應。這樣既簡化了數學模型,方便了分析,同時也不會造成太大的誤差。能很好地反映超聲波電動機的穩態特性,但是在瞬態過程中,由于超聲波電動機的轉速變化較快,剛性連接模型已經不能準確反映系統的轉速變化規律,特別是測試系統一般與光電編碼器通過聯軸節相聯,聯軸節與電機軸和光電編碼
器軸部分的彈性環節必須考慮,為此本文對于一般瞬態特性測試系統用如圖1所示力學模型描述。圖中J1為超聲波電動機轉子和負載的轉動慣量,J2為光電編碼器的轉動慣量,k為聯軸環節(包含轉子軸和光電編碼器軸)的彈性剛度,
根據行波型超聲波電動機的驅動原理,并考慮摩擦力傳遞數學模型[6],可以得到電機的驅動轉矩:
式中:FN為電機的預壓緊力;raV為定轉子摩擦接觸層的平均半徑;μ為摩擦比例常數,μ=ε(υs-υr),依賴于定轉子表面的相對速度;υs為定子表面質點的切向速度;υr為轉子的摩擦層線速度。
1.2起動過程
對于圖1的力學模型,可建立系統起動過程的運動微分方程:
式中:TL為電機的負載力矩,d。、d:為電機和光電編碼器的阻尼系數。
將式(1)代入式(2),并采用微分算子 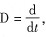 可得: |