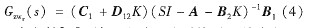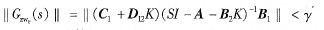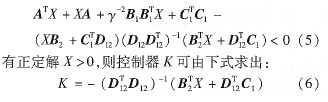交流伺服系統(tǒng)的H∞魯棒控制策略
楊碧石1,劉丙友2
(1.南通職業(yè)大學(xué),江蘇南通226007;2.安徽工程科技學(xué)院,安徽蕪湖241000)
摘要:永磁同步電動(dòng)機(jī)交流伺服控制系統(tǒng)中,擾動(dòng)成為影響系統(tǒng)性能的主要因素,在建立永磁同步電動(dòng)機(jī)魯棒控制模型的基礎(chǔ)上,提出了基于H∞控制理論的標(biāo)準(zhǔn)H∞控制方法,根據(jù)永磁同步電動(dòng)機(jī)的魯棒控制模型設(shè)計(jì)出了魯棒H∞控制器,仿真結(jié)果表明魯棒H∞控制具有良好的魯棒穩(wěn)定性和抗干擾性。
關(guān)鍵詞:永磁同步電動(dòng)機(jī);伺服系統(tǒng);魯棒控制;H∞控制器
中圖分類(lèi)號(hào):TM383.4+1 文獻(xiàn)標(biāo)識(shí)碼:A 文章編號(hào):1004—7018(2008)08-0043—02
0引言
永磁同步電動(dòng)機(jī)(以下簡(jiǎn)稱(chēng)PMSM)矢量控制系統(tǒng)在交流伺服領(lǐng)域得到廣泛應(yīng)用,但這種控制方法要求建立電動(dòng)機(jī)的精確模型,而PMSM的模型是高階次、非線性、強(qiáng)耦合的[1],且在模型的建立過(guò)程中經(jīng)過(guò)了一定的理想假設(shè),所以傳統(tǒng)的控制策略就存在較大的誤差。在微進(jìn)給、精加工等精細(xì)控制領(lǐng)域,擾動(dòng)是造成系統(tǒng)性能下降的主要因素。為了提高系統(tǒng)的性能,必須對(duì)擾動(dòng)進(jìn)行抑制,即對(duì)擾動(dòng)進(jìn)行補(bǔ)償。而系統(tǒng)的擾動(dòng)主要有參數(shù)攝動(dòng)和來(lái)自外部的干擾,交流伺服系統(tǒng)中的擾動(dòng)主要是參數(shù)掇動(dòng)。針對(duì)PMSM在兩相旋轉(zhuǎn)坐標(biāo)系下的數(shù)學(xué)模型,提出了H∞控制理論的魯棒H∞控制策略,通過(guò)對(duì)系統(tǒng)擾動(dòng)的補(bǔ)償,系統(tǒng)具有較好的抗擾性能和跟隨性能以及較高的加工精度。
1標(biāo)準(zhǔn)H∞魯棒控制思想
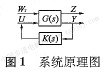
標(biāo)準(zhǔn)H∞魯棒控制的原理結(jié)構(gòu)圖[3,5]如1圖1所示。
圖中:Wr為干擾信號(hào),U為
控制輸入信號(hào),y為被觀測(cè)量信號(hào),z為系統(tǒng)性能評(píng)
價(jià)信號(hào),G(s)增廣被控對(duì)象,K(s)為待設(shè)計(jì)的控制器。
增廣被控對(duì)象G(s)的狀態(tài)空間可表示成如下:
從干擾信號(hào)Wr到評(píng)價(jià)信號(hào)z的閉環(huán)傳遞函數(shù)Gzw(S)可寫(xiě)成:
由文獻(xiàn)[2]可知,此時(shí)上述系統(tǒng)對(duì)于給定的y,存在使閉環(huán)系統(tǒng)是二次穩(wěn)定的狀態(tài)反饋控制器U=KX的充分必要條件是:
且Riccati不等式: 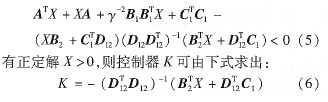 2 H∞控制PMSM的數(shù)學(xué)模型[1]
在做了一定的理想假設(shè)后,PMSM在兩相旋轉(zhuǎn)坐標(biāo)系下的數(shù)學(xué)模型為:
式中:ud、uq、id、iq分別為d軸和g軸的軸電壓、軸電流,ld、lq分別為定子電感在d軸和q軸上的等效電感,Ψf為轉(zhuǎn)子勵(lì)磁磁鏈過(guò)定子繞組的磁鏈,rs為定子電阻,ωe為轉(zhuǎn)子角速度,p為微分算子,p為電動(dòng)機(jī)極對(duì)數(shù),ωm為轉(zhuǎn)子機(jī)械轉(zhuǎn)速,J為轉(zhuǎn)動(dòng)慣量,T1為負(fù)載轉(zhuǎn)矩。
經(jīng)過(guò)整理得PMSM運(yùn)動(dòng)方程為[6]:
永磁同步電動(dòng)機(jī)采用的是轉(zhuǎn)子磁場(chǎng)定向矢量控制方式,控制d軸上的電流id=0,通過(guò)控制q軸上的電流iq即可控制轉(zhuǎn)速,此時(shí)Ψd=Ψf,即可得:
若給定Ψq、ωm值為常數(shù),記為Ψqg、ωmg設(shè)實(shí)際值和設(shè)定值之差為△Ψq=Ψq一Ψqg,△ωm-ωmg,對(duì)其求導(dǎo)可得:
伺服系統(tǒng)中,負(fù)載轉(zhuǎn)矩和定子相電阻都會(huì)有一定的偏差值, |