基于線性化參數(shù)模型的永磁同步電動(dòng)機(jī)參數(shù)估計(jì)

吳茂林，黃聲華

(華中科技大學(xué)，湖北武漢430074)

    摘要：改進(jìn)了永磁同步電動(dòng)機(jī)控制模型并作參數(shù)線性化處理，通過簡單的負(fù)載實(shí)驗(yàn)，對控制模型中的主要參數(shù)，定子電阻R、交直軸電感Ld,Lq和轉(zhuǎn)子永磁磁鏈Фf，利用基于預(yù)報(bào)誤差的參數(shù)估計(jì)方法，在不同負(fù)載條件下估計(jì)了參數(shù)值。結(jié)果表明參數(shù)值隨負(fù)載條件的變化而變化，估計(jì)誤差較小，估計(jì)算法有效，改進(jìn)后可用于參數(shù)的在線辨識。

    關(guān)鍵詞：永磁同步電動(dòng)機(jī)；參數(shù)估計(jì)；線性化模型；實(shí)驗(yàn)

中圖分類號：TM341  文獻(xiàn)標(biāo)識碼：A  文章編號：1004—7018(2008)07一O013—02

    O引  言

    永磁同步電動(dòng)機(jī)(以下簡稱PMSM)已廣泛應(yīng)用

于許多高性能的伺服場合，從控制的角度考慮，系統(tǒng)模型越精確對控制系統(tǒng)性能的提高越有利，也就是說，正確設(shè)計(jì)和優(yōu)化電機(jī)控制系統(tǒng)，控制模型中的參數(shù)必須準(zhǔn)確知道。在轉(zhuǎn)子坐標(biāo)系(d、q軸系)的數(shù)學(xué)模型中，轉(zhuǎn)子磁鏈ψf、定子繞組電阻R和交直軸電感Ld、Lq，隨著系統(tǒng)負(fù)載條件的變化呈時(shí)變特性”。對PMSM模型參數(shù)的確定方法，傳統(tǒng)的方法有直接計(jì)算和實(shí)驗(yàn)測定法。直接計(jì)算法是在電機(jī)制造之前通過計(jì)算估計(jì)，如有限元法；實(shí)驗(yàn)測定法無法直接用在PMSIVI上(PMSM轉(zhuǎn)子磁場無法移去)。PMSM常用的參數(shù)實(shí)驗(yàn)測定方法有直流衰減法、空載和負(fù)載實(shí)驗(yàn)法[1,4]，很多學(xué)者也研究了PMSM的參數(shù)離線估計(jì)和基于控制系統(tǒng)的參數(shù)在線辨識方法[4,7]。本文通過一種簡單的負(fù)載實(shí)驗(yàn)，對控制模型進(jìn)行了線性化改進(jìn)，利用基于預(yù)報(bào)誤差的估計(jì)算法離線估計(jì)了控制模型中的主要參數(shù)。

 

    1線性化參數(shù)模型

PMSM具有正弦形的反電動(dòng)勢波形，其定子電壓、電流也應(yīng)為正弦波，假設(shè)電機(jī)參數(shù)不隨溫度等變化，忽略磁滯、渦流損耗，轉(zhuǎn)子無阻尼繞組，在轉(zhuǎn)子坐  標(biāo)系(d、q軸系)中的數(shù)學(xué)模型為：

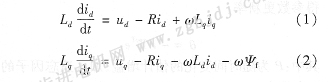
    模型中由于轉(zhuǎn)子速度和交、直軸電流之間相互

耦合，使電機(jī)動(dòng)態(tài)時(shí)模型高度非線性，而且模型中的參數(shù)受系統(tǒng)負(fù)載條件的影響，即Ld、Lq與氣隙磁鏈的飽和程度有關(guān)，定子電阻R和永磁體磁鏈ψ(轉(zhuǎn)矩常數(shù))總是隨著溫度的變化而變化。對于凸極轉(zhuǎn)子的PMSM，直軸磁鏈穿過氣隙和兩次永磁體，交軸磁鏈僅穿過定轉(zhuǎn)子鐵心和氣隙，故交軸電感Lq明顯大于直軸電感Ld，它們受氣隙磁鏈飽和的影響程度和非線性特性也不一樣。

要利用該模型在一般測量基礎(chǔ)上進(jìn)行參數(shù)估計(jì)，同時(shí)能夠體現(xiàn)不同負(fù)載和轉(zhuǎn)速條件下的參數(shù)值，需要對該模型進(jìn)行改進(jìn)，改變模型的輸入輸出，并對參數(shù)作線性化處理，來得到已知測量數(shù)據(jù)和未知參數(shù)之間的線性關(guān)系。雖然對于式(1)的每一項(xiàng)關(guān)于參數(shù)：θ1=[R Ld Lq]和式(2)的每一項(xiàng)關(guān)于參數(shù)：θ2=[R Ld Lq ψf]都是線性的，但式(l)和式(2)要用于參數(shù)估計(jì)還需處理方程中不可直接量測的電流微分量，考慮采用指數(shù)穩(wěn)定的濾波器乘方程兩邊，并作變換后得：

    2參數(shù)估計(jì)算法

基于預(yù)報(bào)誤差的參數(shù)估計(jì)算法[3]，常用的方法包括梯度估計(jì)法、標(biāo)準(zhǔn)最小二乘估計(jì)法和具有指數(shù)遺忘的最小二乘估計(jì)等。利用式(5)進(jìn)行參數(shù)估計(jì)，這幾種估計(jì)算法總是穩(wěn)定的[2]，而加入遺忘因子的標(biāo)準(zhǔn)最小二乘估計(jì)，既能抑制測量噪聲又能估計(jì)，出隨時(shí)間變化的參數(shù)信號，采用該方法的預(yù)測誤差表示為：

    這種算法能保證估計(jì)參數(shù)的收斂性[2]，并對噪聲和干擾有較好的魯棒性，方法簡便實(shí)用。如果不對系統(tǒng)模型進(jìn)行參數(shù)線性化處理，參數(shù)估計(jì)中預(yù)報(bào)誤差準(zhǔn)則將是參數(shù)θ的非線性函數(shù)[5]，所以參數(shù)估計(jì)的優(yōu)化算法需要導(dǎo)出誤差準(zhǔn)則關(guān)于θ的梯度和Hessian矩陣，繁瑣的數(shù)值計(jì)算容易產(chǎn)生計(jì)算誤差，導(dǎo)致參數(shù)估計(jì)的誤差增大。

 

    3實(shí)驗(yàn)及估計(jì)結(jié)果

為能利用各種算法又快又好估計(jì)參數(shù)，除了準(zhǔn)確、合理地建立電機(jī)參數(shù)估計(jì)模型，使其能便于辨識和計(jì)算外，如何得到足夠有用的數(shù)據(jù)，也是參數(shù)估計(jì)過程中關(guān)鍵的一步。同時(shí)，為了提高參數(shù)估計(jì)的精度，設(shè)計(jì)的實(shí)驗(yàn)裝置需考慮在一個(gè)時(shí)間周期內(nèi)連續(xù)的量測得到系統(tǒng)信號，系統(tǒng)信號的變化必須體現(xiàn)系統(tǒng)各種操作條件的特征，以及在不同的負(fù)載條件下