基于卡爾曼濾波器smo的永磁同步電機(jī)無(wú)傳感器矢量控制
劉軍,王剛,俞金壽
(1華東理工大學(xué)信息科學(xué)工程學(xué)院,上海200237;
2上海電機(jī)學(xué)院電氣學(xué)院,上海200240)
摘要:對(duì)永磁同步電機(jī)數(shù)學(xué)模型進(jìn)行深入分析,提出用滑模狀態(tài)觀測(cè)器實(shí)現(xiàn)對(duì)pmsm無(wú)傳感器轉(zhuǎn)子位置和速度估算,引入卡爾曼濾波器,從而使得滑模觀測(cè)器反電勢(shì)波形更加平滑和準(zhǔn)確,也更適合高性能應(yīng)用。用simulink仿真驗(yàn)證了算法的正確性和可行性,并對(duì)結(jié)果進(jìn)行了分析討論。
關(guān)鍵詞:永磁同步電動(dòng)機(jī);滑模觀測(cè)器;卡爾曼濾波器;無(wú)傳感器
o 引 言
在永磁同步電機(jī)(pmsm)矢量控制系統(tǒng)中,通常在轉(zhuǎn)軸上安裝傳感器來(lái)檢測(cè)轉(zhuǎn)子的實(shí)際位置和速度,進(jìn)而實(shí)現(xiàn)轉(zhuǎn)子磁場(chǎng)定向控制。但傳感器增加了系統(tǒng)的成本,降低了系統(tǒng)的可靠性。為了克服機(jī)械傳感器給電機(jī)系統(tǒng)帶來(lái)的缺陷,研發(fā)一種成本低、可靠性好、維護(hù)簡(jiǎn)單的無(wú)位置和速度傳感器的控制方法,便成了電機(jī)控制技術(shù)領(lǐng)域的熱點(diǎn)之一。
目前,估算轉(zhuǎn)子位置角的方法主要有定子磁鏈估算法、模型參考自適應(yīng)法、狀態(tài)觀測(cè)器估算法、人工智能法等,其中大多數(shù)估算方法都需要利用準(zhǔn)確的電機(jī)參數(shù)來(lái)進(jìn)行估算。pmsm是一個(gè)多變量、強(qiáng)耦合、非線(xiàn)性、變參數(shù)的復(fù)雜對(duì)象,且在實(shí)際應(yīng)用中,pmsm是隨運(yùn)行工況變化的。與傳統(tǒng)控制相比,滑模控制對(duì)系統(tǒng)數(shù)學(xué)模型的精確性要求不高,對(duì)于系統(tǒng)的參數(shù)不確定性及外界擾動(dòng)等具有完全魯棒性,滑模控制在交流伺服系統(tǒng)控制領(lǐng)域展示了良好的應(yīng)用前景。本文主要研究基于滑模觀測(cè)器的pmsm系統(tǒng)模型和控制算法,實(shí)現(xiàn)pmsm無(wú)傳感器控制。
l pmsm的坐標(biāo)系和數(shù)學(xué)模型
pmsm調(diào)速控制中,常用的是d-q同步旋轉(zhuǎn)坐標(biāo)系和α-β定子靜止坐標(biāo)系下的數(shù)學(xué)模型,坐標(biāo)系如圖1所示。
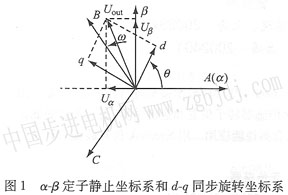
在α-β坐標(biāo)系下,pmsm狀態(tài)方程如下:
電壓方程:
磁鏈方程:
電磁轉(zhuǎn)矩方程:
將式(2)代入式(1)可得:
整理可得:
同理:
當(dāng):
有:
所以α-β定子靜止坐標(biāo)系下的pmsm數(shù)學(xué)模型可以寫(xiě)成:
通常在simulink中p]msm輸出只有靜止坐標(biāo)系abc下的電流值,這樣就需要進(jìn)行坐標(biāo)變換,將其轉(zhuǎn)換到α-β坐標(biāo)系下,然后才能作為滑模觀測(cè)器的輸入進(jìn)行計(jì)算。
2滑模觀測(cè)器實(shí)現(xiàn)位置估算
根據(jù)滑模變結(jié)構(gòu)的理論,對(duì)系統(tǒng):
定義滑模面:
s=s(x)=o (11)
控制函數(shù)為:
只要滿(mǎn)足 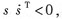 滑模觀測(cè)器就可以在有限的時(shí)間內(nèi)到達(dá)滑模面并在其上進(jìn)行滑模運(yùn)動(dòng)。此時(shí),在滑模面上就有 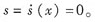 定義pmsm的滑模面為 其中 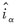 |



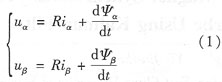
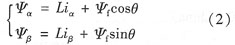
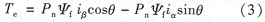
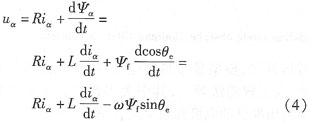
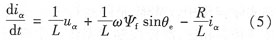
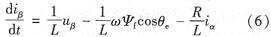
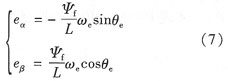
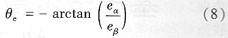
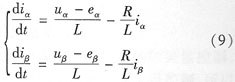
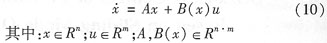
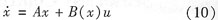
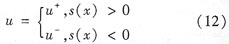
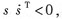 滑模觀測(cè)器就可以在有限的時(shí)間內(nèi)到達(dá)滑模面并在其上進(jìn)行滑模運(yùn)動(dòng)。此時(shí),在滑模面上就有
滑模觀測(cè)器就可以在有限的時(shí)間內(nèi)到達(dá)滑模面并在其上進(jìn)行滑模運(yùn)動(dòng)。此時(shí),在滑模面上就有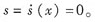 定義pmsm的滑模面為
定義pmsm的滑模面為