基于滑模變結(jié)構(gòu)的異步電機(jī)矢量控制及實(shí)現(xiàn)

鐘義長1，鐘倫瓏2，黃峰1

(1.湖南丁程學(xué)院應(yīng)用技術(shù)學(xué)院，湖南湘潭4111O1；

2.中國民航大學(xué)智能信號(hào)與圖像處理天津市重點(diǎn)實(shí)驗(yàn)室，天津300300)

摘要：擾動(dòng)或負(fù)載的加入對(duì)異步電機(jī)矢量控制系統(tǒng)會(huì)嚴(yán)生影響，使系統(tǒng)性能變差。提出了一種新的方法，介紹了基于滑模變結(jié)構(gòu)的異步電機(jī)矢量控制，對(duì)滑模變結(jié)構(gòu)電流控制器進(jìn)行了設(shè)計(jì)并選取合適的控制參數(shù)。買驗(yàn)與仿真結(jié)果表明滑模變結(jié)構(gòu)控制的異步電機(jī)矢量控制系統(tǒng)動(dòng)靜態(tài)特性良好，具有較強(qiáng)的魯棒性能

關(guān)鍵詞：異步電機(jī)；矢量控制：滑模變結(jié)構(gòu)控制

中圖分類號(hào)：TM343    文獻(xiàn)標(biāo)識(shí)碼：A

    1 引言

 

    交流異步電機(jī)較直流電機(jī)而言，具有結(jié)構(gòu)簡單，輸出轉(zhuǎn)矩大等特點(diǎn)，但是，異步電機(jī)同時(shí)又是一個(gè)多變量、強(qiáng)耦合、非線性的高階時(shí)變系統(tǒng)[1]因而很難直接通過外部信號(hào)來準(zhǔn)確控制其電磁轉(zhuǎn)矩，這樣也就很難適用于控制精度要求高的工業(yè)場合。1971年德國Bladchke F提出的矢量控制理論，通過坐標(biāo)變換將異步電機(jī)模型等效為一臺(tái)直流電機(jī)，因而方便地對(duì)異步電機(jī)實(shí)施控制[2]。傳統(tǒng)PID控制方法可以使伺服系統(tǒng)獲得一定的控制精度，但系統(tǒng)的魯棒性能不佳[3]，近年來，滑模變結(jié)構(gòu)控制方法對(duì)系統(tǒng)參數(shù)變化和外部干擾具有良好的魯棒性，動(dòng)態(tài)響應(yīng)快，并且易于設(shè)計(jì)與實(shí)現(xiàn)。本文通過滑模變結(jié)構(gòu)控制器的設(shè)計(jì)實(shí)現(xiàn)了異步電機(jī)穩(wěn)定、準(zhǔn)確、快速地調(diào)速。

 

    2 異步電機(jī)仿真模型與滑模變結(jié)構(gòu)原理

 

    2.1滑模變結(jié)構(gòu)原理

 

    滑模變結(jié)構(gòu)控制SMVSC)[是變結(jié)構(gòu)控制的一種控制方法，它的控制原理是當(dāng)系統(tǒng)狀態(tài)穿越狀態(tài)空間的不連續(xù)曲面(超平面、開關(guān)平面)時(shí)，反饋控制的結(jié)構(gòu)就發(fā)生變化，迫使系統(tǒng)在一定特性下沿狀態(tài)軌跡作小幅度、高頻率的運(yùn)動(dòng)，以使系統(tǒng)達(dá)到期望的性能指標(biāo)，并且當(dāng)系統(tǒng)進(jìn)入滑模運(yùn)動(dòng)時(shí)，系統(tǒng)參數(shù)的變化或外界擾動(dòng)對(duì)滑模運(yùn)動(dòng)幾乎沒有影響，因而系統(tǒng)就具有良好的自適應(yīng)性與魯棒性。

 

    2.2異步電機(jī)模型

 

    在定子靜止兩相坐標(biāo)系下，異步電機(jī)的電壓一電流模型的狀態(tài)方程[5]描述為：

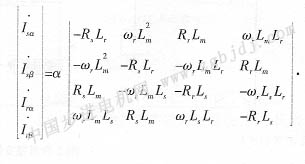
    3 滑模變結(jié)構(gòu)控制器的設(shè)計(jì)

 

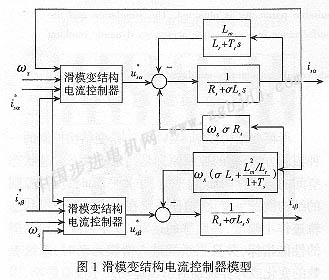
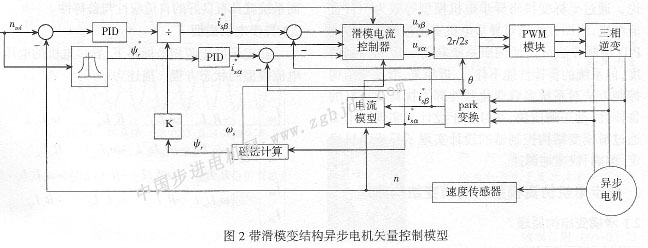
    帶滑模變結(jié)構(gòu)的控制，其關(guān)鍵在于控制器的設(shè)計(jì)，本文采用滑模變結(jié)構(gòu)電流控制器，其結(jié)構(gòu)如圖1所示。帶滑模變結(jié)構(gòu)異步電機(jī)矢量控制模型如圖2所示。

    對(duì)于滑模變結(jié)構(gòu)控制器的設(shè)計(jì)，包括兩個(gè)部分：一是設(shè)計(jì)滑模面，使得滑模面s=O；二是設(shè)計(jì)滑動(dòng)模態(tài)控制率，以保證滑模面以外的運(yùn)動(dòng)點(diǎn)都可以在較短的時(shí)間內(nèi)重瓶回到滑模面上：

    3.1 滑模面s的設(shè)計(jì)

    3.2滑動(dòng)模態(tài)控制率的設(shè)計(jì)

 

    為了消除變結(jié)構(gòu)控制給系統(tǒng)帶來的抖動(dòng)，必須選取合適的增益常數(shù)[5]。在本文中，為了得到恰當(dāng)?shù)脑鲆鏀?shù)值，采用了指數(shù)趨近律：s=εsgn(s)+ks來確定增益常數(shù)。通過對(duì)控制率參數(shù)ε和k的調(diào)整，使系統(tǒng)能夠盡可能的快速到達(dá)滑模面，從而保證系統(tǒng)的穩(wěn)定性與動(dòng)態(tài)品質(zhì)。

 

    令α-β書坐標(biāo)軸下異步電機(jī)的給定電壓滿足：

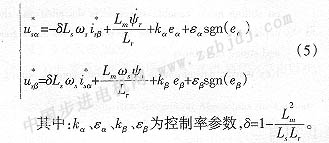
    由李雅普諾夫穩(wěn)定性理論知識(shí)，此時(shí)令該系統(tǒng)的李雅普諾夫函數(shù)為：

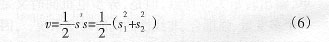
    若系統(tǒng)可以返回滑模面，那么李雅普諾夫函數(shù)的導(dǎo)數(shù)滿足υ<0，即：