BP算法改進及其在股票價格預測中的應用

安靜1，曾成順1,2

（1．廣東松山職業技術學院電氣工程系，廣東韶關512126；

    2．華南理工大學自動化科學與工程學院，廣東廣州510641)

摘要介紹了神經網絡的基本概念，BP算法是前饋神經網絡中最終要的算法模型，但由于BP算法收斂速度慢，為了加速算法收斂，增加神經網絡的穩定性，提出了L-M對股票指數預測模型。借助神經網絡對非線性函數的逼近能力，對上證綜合指數股價進行單步預測。用L-M和BP對預測結果進行比較，證明L-MBP算法用于指標預測準確性更高。

關鍵詞：Levenberg-Marquardt；神經網絡；預測：股票價格

中圖分類號：TP391    文獻標識碼：A

    1 引言

 

    我國股票市場迅速發展，股票投資已成為眾多個人理財的一種重要方式。如何能讓投資者正確預測股票價格，選準買賣時機，無疑成為許多人關注的焦點。經過長期的實踐和研究，如K線法、移動平均線法等。這些方法基本建立在統計學基礎上，雖然簡單，易于掌握，但由于股市運作是一個巨大的非線性的系統，股價走勢受到政治、經濟、心理等眾多因素的影響，使用傳統的技術分析工具進行股票買賣決策難度大，因人而異，差異顯著，一般投資者應用效果不理想。

 

    由于神經網絡具有很強的非線性關系概況能力，它不需要建立復雜的非線性系統的顯式關系或數學模型，用于股市預測取得了一定的效果。但傳統的BP算法具有如下主要缺點：局部極值、收斂速度慢以及難以確定隱節點個數。在實際應用中，BP算法很難勝任，因此從不同角度提出許多改進算法，比如改進誤差函數以避免局部最小值、改進優化方法、激勵函數、網絡結構等以加快網絡收斂。Levenberg-Marquardt算法是牛頓法的變形，用以最小化那些作為其它非線性函數平方和的函數，這非常適合于性能指數是均方誤差的神經網絡訓練。

 

    2 前饋神經網絡算法

 

    2.1前向計算

 

    Levenberg-Marquardt算法中的關鍵一步是求雅可比矩陣的計算，用一種BP算法的變形來進行計算。典型前饋神經網絡的結構包括輸入層、隱層、輸出層，各層之間實行全互連接，層內神經元之間無連接。

 

    設網絡共上層，包括輸入層、隱層和輸出層。

通常取1，輸出范圍為(O，1)，當函數的值接近于0或1時，函數值對自變量的變化不敏感，此時權值的微小變化不會對神經元的輸出產生影響，它所受到后面樣本學習的影響不會很大。如果此時神經元的輸出不是期望的輸出值，而權值的調節量又很小，就很難將該神經元的狀態調整過來，因而影響了網絡的收斂速度，這就是所謂的“平臺”現象。

 

    2.2 LM算法

 

    目標函數為：

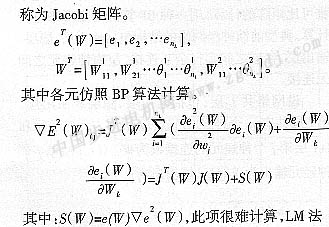
    3 算法流程

 

    實驗表明，結合DFP算法的神經網絡訓練過程在誤差很大或者不是線性函數時具有明顯的優越陛。但如果LM算法的條件滿足即當誤差很小或者誤差使線性函數時，則應用LM算法。如圖1所示為神經網絡算法流程圖。

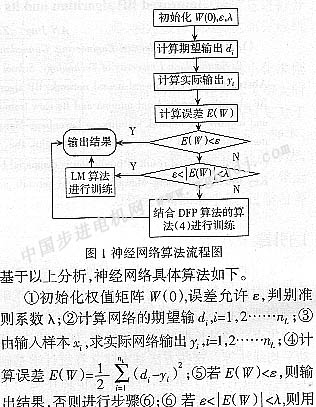
LM算法(3)訓練網絡，否則進行N步驟⑦；⑦用結合DFP算法的神經網絡算法(4)訓練網絡。

 

    4實例分析

 

    本文用訓練后的神經網絡模型作“單步”預測。“單步”預測是每步都使用歷史數據，僅預報第二天的股票指數。例如，輸入數據n1、n2、…n5得到預測值n6。本文利用神經網絡模型對上海證券交易