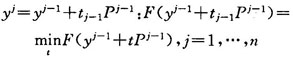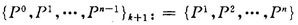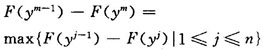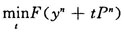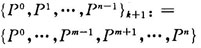基于改進(jìn)鮑威爾法的單相電機(jī)優(yōu)化設(shè)計(jì)

    金明  吳新振(青島大學(xué)山東266071)

    【摘  要】鮑威爾法是一種可用于電機(jī)優(yōu)化設(shè)計(jì)的直接搜索法。通過改進(jìn)后，該法既具有收斂速度快的優(yōu)勢，又避免了原方法不保證各輪迭代中前n個(gè)搜索方向線性無關(guān)的弊病。文中將改進(jìn)的鮑威爾法用于單相電機(jī)優(yōu)化設(shè)計(jì)，取得了令人滿意的結(jié)果。

1  引  言

    電機(jī)的自動(dòng)優(yōu)化設(shè)計(jì)是在****化數(shù)學(xué)理論的基礎(chǔ)上，借助計(jì)算機(jī)以選出****方案的一種設(shè)計(jì)方法。隨著計(jì)算機(jī)性能的不斷提高及優(yōu)化理論的不斷完善，這種設(shè)計(jì)方法得到了越來越廣泛的應(yīng)用。單相電機(jī)只需要單相電源供電，且具有結(jié)構(gòu)簡單、運(yùn)行可靠、維修方便等特點(diǎn)，廣泛應(yīng)用于家用電器、電動(dòng)工具、醫(yī)療器械及輕工設(shè)備中。這種電機(jī)量大面廣、種類繁多、更新?lián)Q代快，因此計(jì)算機(jī)輔助分析計(jì)算及優(yōu)化設(shè)計(jì)顯得尤為重要。

    單相電機(jī)的優(yōu)化設(shè)計(jì)在數(shù)學(xué)上可歸結(jié)為有約束、多變量、非線性的混合性規(guī)劃問題，其目標(biāo)函數(shù)具有多極值點(diǎn)的特性。對該類優(yōu)化問題，目前常用的方法是先通過引入罰函數(shù)將有約束優(yōu)化轉(zhuǎn)化為無約束優(yōu)化，然后再利用直接搜索方法進(jìn)行求解。

    直接搜索方法有很多種，各有其優(yōu)缺點(diǎn)。對于電機(jī)優(yōu)化設(shè)計(jì)，鮑威爾法是比較有效的一種方法。該方法的突出優(yōu)點(diǎn)是收斂速度快，尤其是當(dāng)優(yōu)化變量數(shù)目增多時(shí)更為明顯。本文將改進(jìn)的鮑威爾法用于單相電機(jī)優(yōu)化設(shè)計(jì)的研究，取得了令人滿意的結(jié)果。

2鮑威爾法及其改進(jìn)

    鮑威爾法又稱方向加速法，它是powell以構(gòu)造共軛搜索方向的經(jīng)驗(yàn)為基礎(chǔ)而提出的。原始鮑威爾法的迭代步驟如下：

    第1步  選取初始數(shù)據(jù)。選取初始點(diǎn)x⁰，n個(gè)線性無關(guān)的初始搜索方向{p⁰，p¹，…，p^n-1}₀。，給定終止誤差ε>0，令k:=0。

第2步進(jìn)行基本搜索。令y⁰：=x^k,依次沿{p⁰，p¹，…，p^n-1}_k中的方向進(jìn)行一維搜索。設(shè)對應(yīng)地得到輔助迭代點(diǎn)y¹，y²，…，yⁿ，即

   第3步進(jìn)行加速搜索。令pⁿ=yⁿ-y⁰。若‖pⁿ‖≤ε，停止迭代輸出x^k+1=yⁿ。否則，求解設(shè)得到****解tn，令x^k+1=yⁿ+t_npⁿ。

第4步調(diào)整搜索方向組。在原來n個(gè)方向中，除去p。增添加速方向pⁿ，構(gòu)成新的搜索方向組{p⁰，p¹，…，p^n-1)_k+1，即

  令k：=k+1，轉(zhuǎn)第2步。

  原始鮑威爾法的主要缺點(diǎn)并不保證各輪迭代中前n個(gè)搜索方向的線性無關(guān)性，從而有可能導(dǎo)致求解失敗。為此需對原始鮑威爾法進(jìn)行改進(jìn)。

    第3步構(gòu)造加速方向。令pⁿ=yⁿ-y⁰。若‖pⁿ‖≤ε，停止迭代輸出x^k+1=yⁿ。否則進(jìn)行第4步。

    第4步確定調(diào)整方向。按下式尋找m，使得

若f(y⁰)-2f(yⁿ)+f(2yⁿ-y⁰)<2[f(y^m-1)-f(y^m)]成立，則進(jìn)行第5步。否則，進(jìn)行第6步。

    第5步調(diào)整搜索方向組。求解

設(shè)得到****解tn，令x^k+1=yⁿ+t_npⁿ。同時(shí)，令

    令k：=k+1，轉(zhuǎn)第2步。

    第6步不調(diào)整搜索方向組。完成不使用pⁿ的本輪迭代。令x^k+1：=yⁿ，k：=k+1，轉(zhuǎn)第2步。

3電機(jī)優(yōu)化的數(shù)學(xué)模型

電機(jī)優(yōu)化的數(shù)學(xué)模型可歸納為：在滿足約束條件g_i(x)≤0的情況下，求各變量x_i(i=1，2，…，n)的值，使目標(biāo)函數(shù)f(x)最小。式中x=(x₁，x₂，…，x_n)^t。