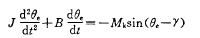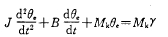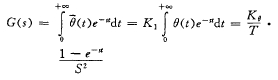摘要：對(duì)步進(jìn)電機(jī)在航空發(fā)動(dòng)機(jī)數(shù)控系統(tǒng)中的應(yīng)用進(jìn)行了研究，提出了以步進(jìn)電機(jī)和計(jì)算機(jī)所構(gòu)成的步進(jìn)電機(jī)系統(tǒng)的數(shù)學(xué)模型，分析了步進(jìn)電機(jī)對(duì)航空發(fā)動(dòng)機(jī)轉(zhuǎn)速數(shù)控系統(tǒng)的影響，給出了系統(tǒng)采樣周期的選擇依據(jù)，得出了一些有益的結(jié)論．

關(guān)鍵詞：步進(jìn)電機(jī)i數(shù)字控制#采樣周期

中圖分類號(hào)：tm383.6    文獻(xiàn)標(biāo)識(shí)碼；a    文章編號(hào)：1001-6848(2000)01-0021-03

    在發(fā)動(dòng)機(jī)數(shù)控系統(tǒng)中，步進(jìn)電機(jī)是一個(gè)重要的執(zhí)行元件，其性能直接影響了整個(gè)控制系統(tǒng)的品質(zhì)指標(biāo)。有關(guān)步進(jìn)電機(jī)的研究目前多著眼于電機(jī)本身，而沒(méi)有將電機(jī)與計(jì)算機(jī)控制系統(tǒng)聯(lián)系起來(lái)考慮，所建立的數(shù)學(xué)模型階次很高，往往是一組非線性微分方程組，這對(duì)發(fā)動(dòng)機(jī)數(shù)字控制器的設(shè)計(jì)是十分不便的。基于微機(jī)控制的步進(jìn)電機(jī)系統(tǒng)在工業(yè)過(guò)程中雖有應(yīng)用，但被調(diào)對(duì)象與航空發(fā)動(dòng)機(jī)相比一般變化較慢，因而將其作為響應(yīng)要求較高的航空發(fā)動(dòng)機(jī)數(shù)控系統(tǒng)的執(zhí)行元件有必要對(duì)其數(shù)學(xué)描述及其拄制性能進(jìn)行專門研究。

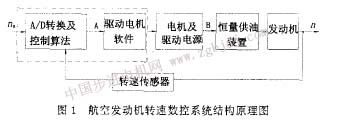
    以步進(jìn)電機(jī)作為執(zhí)行元件的航空發(fā)動(dòng)機(jī)轉(zhuǎn)速數(shù)控系統(tǒng)結(jié)構(gòu)原理如圖1所示[1]。

    該系統(tǒng)中，步進(jìn)電機(jī)是由計(jì)算機(jī)控制的，虛線為計(jì)算機(jī)內(nèi)部軟件部分。步進(jìn)電機(jī)系統(tǒng)指的是圖l中a點(diǎn)到b點(diǎn)的各環(huán)節(jié)。求取步進(jìn)電機(jī)系統(tǒng)的數(shù)學(xué)模型既描述了電機(jī)本身的動(dòng)特性，又描述了計(jì)算機(jī)與步進(jìn)電機(jī)的聯(lián)系，這樣求取的模型具有應(yīng)用性，可直接用于具有該執(zhí)行機(jī)構(gòu)的系統(tǒng)中。一個(gè)理想的步進(jìn)電機(jī)空載時(shí)的運(yùn)動(dòng)方程為[2]：

  單步響應(yīng)失調(diào)角θe-γ變化不大，故sin (θe -γ)≈θe-γ，代入止式，得：

  可知，當(dāng)步進(jìn)電機(jī)接受一個(gè)脈沖時(shí)，由于一般線性阻尼系數(shù)較小，所以電機(jī)的響應(yīng)是一個(gè)衰減的振蕩過(guò)程。

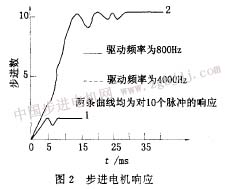
    步進(jìn)電機(jī)多數(shù)情況是接受一連串脈沖的、連續(xù)步進(jìn)的，其多步響應(yīng)一般并不是單步響應(yīng)的簡(jiǎn)單迭加，這取決于驅(qū)動(dòng)脈沖頻率的大小。頻率不同，對(duì)電機(jī)轉(zhuǎn)動(dòng)的影響也就不同。在較低頻范圍內(nèi)（驅(qū)動(dòng)電源在步進(jìn)電機(jī)每步進(jìn)一步完全穩(wěn)定后，才發(fā)出一個(gè)驅(qū)動(dòng)脈沖），可以認(rèn)為多步響應(yīng)是單步響應(yīng)的迭加。圖2是步進(jìn)電機(jī)系統(tǒng)多步響應(yīng)曲線。曲線1表示步進(jìn)電機(jī)在高于電機(jī)****啟動(dòng)頻率下運(yùn)行的響應(yīng)，可看出，在該頻率下工作，電機(jī)可造成失步；曲線2表示步進(jìn)電機(jī)在低于****啟動(dòng)頻率、低頻共振區(qū)之外（頻率若在低頻共振區(qū)之內(nèi)，易失步）的頻率驅(qū)動(dòng)下的響應(yīng)，可看出，電機(jī)幾乎可以不失步地運(yùn)行。

    在發(fā)動(dòng)機(jī)數(shù)控系統(tǒng)中，每個(gè)采樣間隔內(nèi)，步進(jìn)電機(jī)系統(tǒng)都將接受一個(gè)控制作用量，該控制量可以看作一個(gè)強(qiáng)度由控制算法的計(jì)算所確定的脈沖，脈沖強(qiáng)度與該采樣周期內(nèi)步進(jìn)電機(jī)應(yīng)走的步數(shù)相對(duì)應(yīng)。此時(shí)，步進(jìn)電機(jī)系統(tǒng)對(duì)該脈沖的響應(yīng)是一個(gè)多步響應(yīng)。由此根據(jù)圖2的曲線2，可以近似認(rèn)為，其脈沖響應(yīng)如圖3所示。圖3中的口角是隨脈沖強(qiáng)度而變化的，t為采樣周期。

    設(shè)g(s)為步進(jìn)電機(jī)系統(tǒng)的傳遞函數(shù)。

    θ(t)為系統(tǒng)的單位脈沖響應(yīng)。

    θ(f)為系統(tǒng)的脈沖響應(yīng)。

    則θ(t)=k1θ(t)，由線性系統(tǒng)脈沖響應(yīng)的性質(zhì)得其步進(jìn)電機(jī)系統(tǒng)的數(shù)學(xué)模型為；

    (1)步進(jìn)