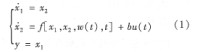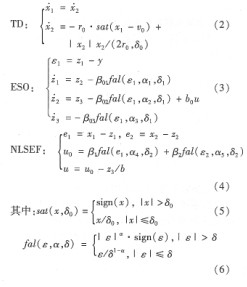自抗擾控制器優(yōu)化設(shè)計及其應(yīng)用
孫亮,吳根忠
(浙江工業(yè)大學信息工程學院,浙江杭州310032)
摘要:自抗擾控制器( adrc)是針對非線性不確定系統(tǒng)提出的一種新型非線性控制器。在深入研究自抗擾控制技術(shù)理論的基礎(chǔ)上,通過非線性系統(tǒng)的線性化和參數(shù)整合等方法設(shè)計出了優(yōu)化adrc,并給出了新的參數(shù)整定方法。matlab仿真表明,優(yōu)化后的adrc需調(diào)整的參數(shù)大大減少,調(diào)節(jié)過程也得到簡化,但性能并未受到影響,對被控系統(tǒng)的不確定性和外擾有很強的適應(yīng)性和魯棒性。
關(guān)鍵詞:自抗擾控制器;優(yōu)化算法;交流伺服系統(tǒng)
中圖分類號:tm571 文獻標識碼:a文章編號:1673-6540(2010)03-0026-05
0 引 言
自抗擾控制器…( adrc)是中國科學院韓京清研究員提出的一種新型的非線性魯棒控制器。adrc不依賴于被控對象的精確數(shù)學模型,具有魯棒性強、系統(tǒng)響應(yīng)快、抗干擾能力強等優(yōu)點,有效地解決了系統(tǒng)快速性和超調(diào)之間的矛盾。近年來控制器已經(jīng)在風力發(fā)電系統(tǒng)、混沌控制、電機拖動、飛行器姿態(tài)控制等領(lǐng)域得到廣泛應(yīng)用,其控制器本身也得到了進一步的完善和發(fā)展,出現(xiàn)了基于神經(jīng)網(wǎng)絡(luò)的adrc,變結(jié)構(gòu)adrc等各種改進型控制器。
adrc的三個組成部分均采用非線性函數(shù),參數(shù)較多,調(diào)節(jié)繁雜,在還沒有成熟的參數(shù)整定理論條件下,參數(shù)整定過程和效果在很大程度上依賴于人們的經(jīng)驗。因此,控制器優(yōu)化和參數(shù)整定問題成為制約adrc發(fā)展的瓶頸。通過優(yōu)化算法,可以在保證控制效果的前提下極大地簡化adrc參數(shù)的調(diào)節(jié)過程,從而使得控制器更適合實際工業(yè)控制的要求,擴展了控制器的應(yīng)用范圍。
交流伺服系統(tǒng)有較高的性能指標要求,特別在永磁同步電機( pmsm)位置伺服系統(tǒng)中,pmsm作為一個多變量、非線性和強耦合的被控對象.具有非線性和不確定性,以及混沌運動特性,實現(xiàn)高性能的伺服系統(tǒng)控制,必須依靠高性能的控制器,尤其在快速性、準確性等要求較高的場合,先進的控制策略就更為重要了。將優(yōu)化的adrc用于pmsm伺服系統(tǒng)中,不僅算法簡單,參數(shù)容易調(diào)節(jié),而且對系統(tǒng)參數(shù)變化和外部干擾具有很強的魯棒性,提高了伺服系統(tǒng)的控制精度。
1adrc典型結(jié)構(gòu)
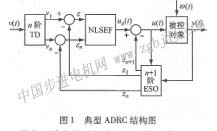
adrc是在反饋線性化基礎(chǔ)上設(shè)計的新型控制器,其實質(zhì)是利用“觀測+補償”的方法來處理系統(tǒng)中非線性和不確定性,同時配合非線性的反饋方式,提高控制器的動態(tài)性能。控制器由跟蹤微分器(td)、擴張狀態(tài)觀測器(eso)和非線性反饋控制律( nlsef)三部分組成,圖l為典型ad-rc結(jié)構(gòu)圖。
設(shè)含不確定擾動的非線性被控對象:
其中f為未知的非線性時變函數(shù),w(t)為外部擾動,u(t)為控制輸入,b為模型參數(shù),根據(jù)自抗擾理論可以設(shè)計的adrc算法結(jié)構(gòu)如下。
由式(2)~(6)可知,adrc的調(diào)節(jié)參數(shù)主要包括td的{r0,δ0},eso部分中的{β01,β02,β03,αl,α2,α3,δ1,b0},nlsef中的{β1,β2,α4,α5,δ2}。這些參數(shù)的確定是一項繁雜的過程,而且目前參數(shù)調(diào)整主要還靠經(jīng)驗,因此在實際使用時調(diào)節(jié)復(fù)雜,不利于廣泛應(yīng)用。
2 adrc的優(yōu)化算法
典型的adrc模型采用誤差的非線性比例、微分調(diào)節(jié),理論上可以實現(xiàn)較好的控制性能,但實際由于整定參數(shù)個數(shù)多,算法實現(xiàn)需要較大計算量,導致控制周期變長,影響了控制器的性能。
2.1優(yōu)化算法設(shè)計及參數(shù)整定
將典型adrc三個組成部分進行線性簡化和參數(shù)整合,建立其優(yōu)化的adrc,并通過仿真驗證優(yōu)化后結(jié)構(gòu)的有效性及可行性,突破了adrc工業(yè)應(yīng)用的限制。
對于式(1)根據(jù)跟蹤微分器的基本結(jié)論,可以得出式(7)也是有效的非線性跟蹤微分器,將其線性化可以得出線性跟蹤微分器算法結(jié)構(gòu)為式(8)。 |