摘    要：針對船舶動態性能具有較強的非線性、大慣性及時變性的特點，采用具有rbf核函數的最小二乘支持向量機( ls-svm)，利用其可以任意逼近非線性模型的良好特性實現對船舶模型有效辨識，得到船舶航向控制系統的非線性逼近模型，并將其與模型預測控制方法相結合，將最小二乘支持向量機辨識得到的系統模型作為預測模型，并將系統模型進行線性化并用線性預測控制方法求得解析的控制律，實現對船舶航向的預測控制，達到良好航向保持目的。仿真結果表明，最小二乘支持向量機降低了計算復雜度，且有較快計算速度，在小樣本情況下具有良好的泛化能力；基于最小二乘支持向量機的船舶航向預測控制系統對外界干擾及模型參數攝動均具有較好的適應能力以及艮好的控制性能。

關鍵詞：最小二乘；支持向量機；船舶航向；模型預測控制

中圖分類號：tp 27    文獻標識碼：a

  船舶航向控制是評判船舶操縱性能好壞的重要標準，航向控制系統性能關系著船舶航行的經濟性和安全性。而船舶在海上航行時所受的擾動比較復雜，且沒有自身航向穩定性，為保證船舶按照期望航向航行，必須通過控制系統控制轉舵以校正由于擾動而產生的偏航。

  模型預測控制是20世紀80年代初發展起來的拉制算法，利用動態模型預測系統未來行為

并根據模型對系統進行優化控制，具有控制效果好、魯棒性強及對模型精度要求不高等優點，是具有代表性的預測控制算法。由于船舶參數具有較強的非線性，并且裝載變化等會引起參數攝動，不易建立準確的數學模型，因此本文選擇利用最小二乘支持向量機54-( ls-svm)解決航向非線性建模問題，與傳統支持向量機相比，避免了求解qp方程，學習速度快，且具有較好的推廣性和很強的魯棒性，有效防止過學習現象。將得到的航向非線性逼近模型應用于模型預測控制算法，采用多步預測、滾動優化及反饋校正等控制策略，得到較好的船舶航向控制效果。

    1)船舶數學模型  在k-t模型基礎上加入一個非線性項，以描述舵角，航向角為主，省略了橫漂速度，即有：

 

  2)基于最小二乘的支持向量機系統辨識支持向量機結構，如圖1所示。

   

    通過非線性映射將樣本空間中的非線性函數轉化為高維空間中，即找一個非線性函數φ (x)使輸入通過它后得到的非線性函數，能逼近輸入與輸出之間的關系，這樣難以在樣本空間中直接計算的****超平面就轉化到在輸入空間中求解一個凸約束條件下的凸規劃問題。

    在支持向量機中加入誤差的平方項ek²即得到最小二乘支持向量機。

ls-svm的優化問題為

 

    為解上述優化問題，引入拉格朗日函數：

    根據kkt條件求解上式，即令l偏導為零，得到解析解為

    式(5)選擇rbf作為核函數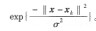：其中，δ為核寬度。

    3)支持向量機的系統辨識實現  以某時刻舵角δ(k)為系統輸入u(k)，航向角ψ(k)為輸出y（k），選取支持向量機預測模型輸入、輸出分別為u，y，如圖2所示。

   

    某船舶模型參數是：t1=1，t2=0.5，t3=5，a=3，kb=0.1，產生100組輸入輸出數據作為訓練最小二乘支持向量機的樣本，參數設為σ2=100，c