摘    要：針對(duì)無軸承異步電機(jī)轉(zhuǎn)子徑向兩自由度懸浮系統(tǒng)的相互耦合情況，采用神經(jīng)網(wǎng)絡(luò)逆系統(tǒng)方法進(jìn)行了動(dòng)態(tài)解耦控制研究。在介紹無軸承異步電機(jī)工作原理的基礎(chǔ)上，建立了無軸承異步電機(jī)徑向懸浮力的數(shù)學(xué)模型，對(duì)該模型進(jìn)行可逆性分析，證明該系統(tǒng)可逆，應(yīng)用神經(jīng)網(wǎng)絡(luò)逆系統(tǒng)方法將原來多變量、強(qiáng)耦合的非線性系統(tǒng)，動(dòng)態(tài)解耦成2個(gè)位置彼此無耦合的線性子系統(tǒng)，并對(duì)解耦后的線性子系統(tǒng)進(jìn)行了閉環(huán)設(shè)計(jì)：最后利用Matlab/Simulink工具箱對(duì)該控制系統(tǒng)作了仿真研究。仿真試驗(yàn)結(jié)果顯示，神經(jīng)網(wǎng)絡(luò)逆系統(tǒng)方法可保證無軸承異步電機(jī)在徑向兩自由度上實(shí)現(xiàn)獨(dú)立控制，且閉環(huán)系統(tǒng)具有良好的動(dòng)、靜態(tài)性能。

關(guān)鍵詞：無軸承異步電機(jī)；徑向位置；神經(jīng)網(wǎng)絡(luò)逆；解耦控制

中圖分類號(hào)：TP 27    文獻(xiàn)標(biāo)識(shí)碼：A

    利用磁軸承和電機(jī)結(jié)構(gòu)的相似性，把磁軸承中的懸浮繞組疊繞在電機(jī)定子繞組上，使兩種磁場(chǎng)合成一體，且能同時(shí)獨(dú)立控制電機(jī)轉(zhuǎn)子的懸浮和旋轉(zhuǎn)。無軸承電機(jī)正是基于這一設(shè)想而提出的，無軸承電機(jī)的種類很多，有永磁型、感應(yīng)型、磁阻型等，其中，結(jié)構(gòu)簡(jiǎn)單、易于弱磁、可靠性高的無軸承異步電機(jī)尤其受到廣泛的重視。

    由于無軸承電機(jī)的懸浮是定子上轉(zhuǎn)矩繞組和懸浮繞組相互作用的結(jié)果，電機(jī)懸浮力和電磁轉(zhuǎn)矩之間、懸浮力之間存在著復(fù)雜的非線性耦合關(guān)系，因此要實(shí)現(xiàn)電機(jī)高性能穩(wěn)定運(yùn)行并有較高的控制性能，必須對(duì)電機(jī)進(jìn)行非線性解耦。文獻(xiàn)[5]采用轉(zhuǎn)子磁場(chǎng)定向控制策略對(duì)無軸承異步電機(jī)進(jìn)行丁穩(wěn)定懸浮控制研究，并取得了不錯(cuò)的效果，但是這種控制是一種穩(wěn)態(tài)解耦控制，為了實(shí)現(xiàn)動(dòng)態(tài)解耦，本文采用神經(jīng)網(wǎng)絡(luò)逆系統(tǒng)方法。對(duì)無軸承異步電機(jī)徑向位置系統(tǒng)進(jìn)行動(dòng)態(tài)解耦控制。

    無軸承異步電機(jī)定子中復(fù)合疊繞著尸，對(duì)極的轉(zhuǎn)矩繞組和P，對(duì)極的徑向力繞組，兩套繞組的極對(duì)數(shù)應(yīng)滿足以下關(guān)系：P1=P2±1。其中，P1為轉(zhuǎn)矩繞組的極對(duì)數(shù)，P2為懸浮力繞組的極對(duì)數(shù)。且P1=2，由繞組NL1和NL2。構(gòu)成，用來產(chǎn)生旋轉(zhuǎn)磁場(chǎng)和電磁力矩；P2=1，由繞組Nu和Nv構(gòu)成，用來產(chǎn)生徑向懸浮力。在轉(zhuǎn)矩繞組和懸浮控制繞組中分別通人電流i1，i2，則分別產(chǎn)生四極磁鏈ψ1和兩極磁鏈ψ2。x，y代表互相垂直的轉(zhuǎn)子位置控制坐標(biāo)軸，如圖1所示。

   

    在空載情況下，如轉(zhuǎn)子需要沿z正方向的徑向力，在徑向力控制繞組中通入如圖l所示的電流l2。從圖l可得，由于在氣隙右側(cè)ψ1和ψ2同向，則氣隙磁密增加，在氣隙左側(cè)ψ1和ψ2反向，則氣隙磁密減少，從而產(chǎn)生沿x正方向的徑向力Fa。在懸浮控制繞組中通入反相電流，可產(chǎn)生沿x反方向的徑向力。同理，沿y軸方向的徑向力可以通過在懸浮控制繞組中通入與L2垂直的電流獲得。

    為分析方便，通過C3/2和Cr/s變換，將靜止坐標(biāo)系下的3相轉(zhuǎn)換為旋轉(zhuǎn)坐標(biāo)系下的2相研究。在空載情況下，旋轉(zhuǎn)坐標(biāo)系的2相坐標(biāo)相互垂直，轉(zhuǎn)矩繞組和徑向力繞組各自的互感為0。轉(zhuǎn)矩繞組自感L1s和徑向力繞組的自感L2s為常值，二者間的互感M12s與轉(zhuǎn)子的徑向偏移成比例，即

式中，R和l分別為轉(zhuǎn)子半弳和轉(zhuǎn)子軸向長(zhǎng)度；μ0為空氣磁導(dǎo)率；g 0為氣隙長(zhǎng)度；N1，和N2分別為轉(zhuǎn)矩繞組和懸浮力繞組匝數(shù)。

    電機(jī)的電感矩陣rL]可表示如下。

式中α和β分別為轉(zhuǎn)子在x和y方向上的徑向偏移；M為轉(zhuǎn)矩繞組和徑向力繞組的互感系數(shù)；下標(biāo)s表示定子側(cè)的分量。

  根據(jù)能量轉(zhuǎn)換關(guān)系，無軸承電機(jī)儲(chǔ)存的磁能表達(dá)式為

        

式中，[i]=[id1s，iq1s，id2s，iq2s]^T為電流矩陣id1s，iq1s分別為轉(zhuǎn)矩繞組電流在d，q軸上的分量id2s，iq2s為徑向力繞組電流在d，q軸上的分量。

  將變量代人式(3)可得：

    如不考慮磁飽和，根據(jù)虛位移原理，電磁力可表示為電磁儲(chǔ)能對(duì)位移的偏導(dǎo)，因而x和y方向的徑向力可以表示為

另外，根據(jù)電磁場(chǎng)理論，當(dāng)電機(jī)轉(zhuǎn)子偏心時(shí)，轉(zhuǎn)子還受到和偏心位移成正比的麥克斯韋力徑向力fx，fy它是一種固有的力，通常稱為外界力，其是達(dá)式為

 

式中，Ks為徑向位移剛度；x，y分別為轉(zhuǎn)子徑向兩自由度的徑向位移。

    根據(jù)運(yùn)動(dòng)方程，轉(zhuǎn)子的徑向懸浮力控制模型為

式中，m為轉(zhuǎn)子質(zhì)量；g為重力加速度。

    模型可以改寫成：

   選取狀態(tài)變量：

 

  輸入變量：

  輸出變量：

   因此可得系統(tǒng)的狀態(tài)方程為

    對(duì)模型進(jìn)行可逆性分析，首先計(jì)算輸出對(duì)時(shí)間的導(dǎo)數(shù)，直至方程中顯含輸入變量。由式(9)得：

    由于det(A)=-M(i_d1s²+i_q1s²)／m≠O，所以系統(tǒng)可逆。系統(tǒng)的相對(duì)階數(shù)α=(α1，α2)=(2，2)，且α1十α2=2+2=4=n。由隱函數(shù)定理可得，式(8)的逆系統(tǒng)可表示為

  本文采用靜態(tài)神經(jīng)網(wǎng)絡(luò)加積分器s-l來構(gòu)造無軸承異步電機(jī)徑向懸浮力系統(tǒng)的神經(jīng)網(wǎng)絡(luò)逆，并通過調(diào)整靜態(tài)神經(jīng)網(wǎng)絡(luò)的權(quán)系數(shù)使神經(jīng)網(wǎng)絡(luò)實(shí)現(xiàn)被控對(duì)象的逆系統(tǒng)功能；并將神經(jīng)網(wǎng)絡(luò)逆置于原系統(tǒng)之前，神經(jīng)網(wǎng)絡(luò)逆與無軸承異步電機(jī)徑向懸浮力系統(tǒng)組成偽線性系統(tǒng)，其輸入輸出關(guān)系是線性的、解耦的。偽線性系統(tǒng)等效成二個(gè)位置二階積分型的偽線性子系統(tǒng)，其結(jié)構(gòu)，如圖2所示。

  

   

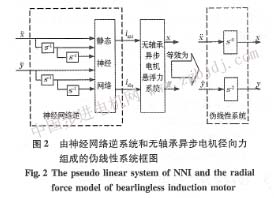
  在辨識(shí)無軸承異步電機(jī)徑向懸浮力系統(tǒng)的神經(jīng)網(wǎng)絡(luò)逆系統(tǒng)時(shí)，本文選用了三層前饋網(wǎng)絡(luò)，輸入節(jié)點(diǎn)數(shù)為6，隱含節(jié)點(diǎn)數(shù)為13，輸出層節(jié)點(diǎn)數(shù)為2，隱層神經(jīng)元激活函數(shù)使用S型函數(shù)，輸出層由具有線性闖值激勵(lì)函數(shù)的神經(jīng)元組成。在確定了神經(jīng)網(wǎng)絡(luò)逆系統(tǒng)的結(jié)構(gòu)后，還需對(duì)神經(jīng)網(wǎng)終逆系統(tǒng)進(jìn)行學(xué)習(xí)、訓(xùn)練。訓(xùn)練神經(jīng)網(wǎng)絡(luò)逆系統(tǒng)的實(shí)質(zhì)是訓(xùn)練神經(jīng)網(wǎng)絡(luò)逆系統(tǒng)中的靜態(tài)神經(jīng)網(wǎng)絡(luò)，使靜態(tài)神經(jīng)網(wǎng)絡(luò)真正實(shí)現(xiàn)其要逼近的非線性運(yùn)算式(Il)。一旦靜態(tài)神經(jīng)網(wǎng)絡(luò)能達(dá)到此目的，則由靜態(tài)神經(jīng)網(wǎng)絡(luò)加積分器構(gòu)成的神經(jīng)網(wǎng)絡(luò)逆系統(tǒng)就真正成為被控系統(tǒng)的逆系統(tǒng)。

    對(duì)于無軸承異步電機(jī)徑向懸浮力系統(tǒng)來說，系統(tǒng)的相對(duì)階為α=(α1，α2)=(2，2)，其輸入為旋轉(zhuǎn)坐標(biāo)系中的電流分量，由于幾個(gè)控制量之間存在一定約束關(guān)系，如只是在無軸承異步電機(jī)徑向懸浮力模型輸入端加隨機(jī)信號(hào)來進(jìn)行開環(huán)采樣是不能得到有效的訓(xùn)練數(shù)據(jù)的。為此，可以通過對(duì)無軸承異步電機(jī)徑向懸浮力系統(tǒng)進(jìn)行閉環(huán)解析逆解耦控制來得到原始訓(xùn)練數(shù)據(jù)。由辨識(shí)的方法來構(gòu)造無軸承異步電機(jī)徑向懸浮力系統(tǒng)的神經(jīng)網(wǎng)絡(luò)逆系統(tǒng)，每組訓(xùn)練數(shù)據(jù)包括6個(gè)神經(jīng)網(wǎng)絡(luò)的輸入信號(hào)，2個(gè)輸出信號(hào)i_d1s, i_q1s，其中，神經(jīng)網(wǎng)絡(luò)輸出信號(hào)的d軸分量和q軸分量可在解析逆解耦控制中直接得到，而輸入信號(hào)的一、二階導(dǎo)數(shù)則是采用高精度采用五點(diǎn)求導(dǎo)算法離線計(jì)算得到，系統(tǒng)的訓(xùn)練。

   

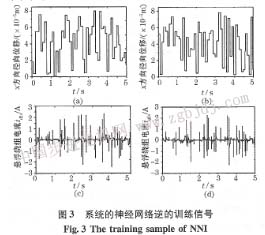
    轉(zhuǎn)子位置輸入給定帽值范圍為0~ 0.08 mm的正態(tài)分布的隨機(jī)量。為使采樣數(shù)據(jù)同時(shí)包含系統(tǒng)響應(yīng)的動(dòng)態(tài)和穩(wěn)態(tài)信息，給定信號(hào)值的持續(xù)時(shí)間應(yīng)足夠長(zhǎng)，仿真中取轉(zhuǎn)子位置給定持續(xù)時(shí)間為0.1 s。為使無軸承異步電機(jī)的輸出信號(hào)不至于有太大的變化率，在隨機(jī)產(chǎn)生的正態(tài)分布的輸入給定值通道上分別設(shè)置了一個(gè)二階數(shù)字濾波器，用于平滑輸入信號(hào)。信號(hào)的采樣步長(zhǎng)取為0 001 s，共取得5 000組數(shù)據(jù)，從中等間隔地抽取3 000組作為網(wǎng)絡(luò)訓(xùn)練數(shù)據(jù)．另外2 000組作為檢驗(yàn)數(shù)據(jù)。但實(shí)際應(yīng)用中，采樣獲得的原始數(shù)據(jù)不是一個(gè)數(shù)量級(jí)，因此采用歸一化處理，將數(shù)據(jù)歸一化到-1~ +1對(duì)訓(xùn)練樣本集做歸一化處理，利于神經(jīng)網(wǎng)絡(luò)訓(xùn)練的收斂，可避免神經(jīng)網(wǎng)絡(luò)對(duì)某一輸入量特別靈敏或不靈敏。

    再采用帶動(dòng)量項(xiàng)和變學(xué)習(xí)率的誤差反傳BP算法對(duì)靜態(tài)神經(jīng)網(wǎng)絡(luò)進(jìn)行訓(xùn)練，確定靜態(tài)神經(jīng)網(wǎng)絡(luò)權(quán)系數(shù)。由于神經(jīng)網(wǎng)絡(luò)具有泛化的功能，所以其對(duì)于未用于訓(xùn)練的樣本集中的輸入也能給出合適的輸出，因此具有強(qiáng)魯棒性和容錯(cuò)性。

    對(duì)由神經(jīng)網(wǎng)絡(luò)逆系統(tǒng)與無軸承異步電機(jī)徑向懸浮力串聯(lián)得到的偽線性系統(tǒng)，再附加線性閉環(huán)控制器來對(duì)其實(shí)現(xiàn)更有效的控制，線性閉環(huán)控制器可采用針對(duì)單變量的線性系統(tǒng)理論中的PID控制、極點(diǎn)配置或二次型指標(biāo)最憂等控制方法。本文選用PD調(diào)節(jié)器Gs(s)=1 100 +45s作為徑向位置調(diào)節(jié)器。

    神經(jīng)網(wǎng)絡(luò)逆系統(tǒng)用靜態(tài)神經(jīng)網(wǎng)絡(luò)逼近式(11)逆系統(tǒng)非線性映射，4個(gè)積分器表征逆系統(tǒng)動(dòng)態(tài)特性。

    無軸承永磁同步電機(jī)徑向懸浮力系統(tǒng)的神經(jīng)網(wǎng)絡(luò)逆解耦控制結(jié)構(gòu)圖，如圖4所示。

 

    以實(shí)驗(yàn)樣機(jī)為研究對(duì)象，通過計(jì)算機(jī)仿真進(jìn)一步驗(yàn)證本文提出的控制策略。系統(tǒng)的參數(shù)如下：功率為1 kW，電機(jī)氣隙為2 mm，輔助機(jī)械軸承氣隙為0 5 mm，轉(zhuǎn)子電感為16. 778×10-2 H，定、轉(zhuǎn)子之間的互感為15. 856 x10^-2H，定子轉(zhuǎn)矩繞組和徑向力繞組互感系數(shù)為78.2 H/m，轉(zhuǎn)子電阻為11. 48 Ω，轉(zhuǎn)子時(shí)間常數(shù)為1.46×10^-2s，轉(zhuǎn)子質(zhì)量為2. 85 kg，轉(zhuǎn)動(dòng)慣量為0 007 69kg．m2，轉(zhuǎn)矩繞組的級(jí)對(duì)數(shù)為2，懸浮力繞組的級(jí)對(duì)數(shù)為l。

  在仿真實(shí)驗(yàn)中，為驗(yàn)證本文所提方法的有效性，對(duì)比逆系統(tǒng)解耦控制，研究了神經(jīng)網(wǎng)絡(luò)逆系統(tǒng)解耦控制的特點(diǎn)。系統(tǒng)的給定在不同的時(shí)刻發(fā)生變化，t=1.5 s時(shí)，徑向x軸位移給定從-0 015 mm變化到0 015 mm;t=1.0 s對(duì)，徑向y軸位移給定從0. 020 mm變化到0010 mm。逆系統(tǒng)方法和ANN逆系統(tǒng)方法在上述條件下的對(duì)比仿真響應(yīng)曲線如圖5所示。

   

    由圖可知，控制一個(gè)輸入只影響一個(gè)輸出，說明系統(tǒng)實(shí)現(xiàn)了解耦的目的。同時(shí)，采用ANN逆系統(tǒng)方法比采用逆系統(tǒng)方法系統(tǒng)的響應(yīng)更快，超調(diào)和穩(wěn)態(tài)誤差更小，系統(tǒng)具有良好的動(dòng)靜態(tài)特性。因此，神經(jīng)網(wǎng)絡(luò)逆系統(tǒng)方法要優(yōu)于逆系統(tǒng)方法。

  針對(duì)無軸承異步電機(jī)這個(gè)多變量、強(qiáng)耦合的非線性系統(tǒng)，提出了基于神經(jīng)網(wǎng)絡(luò)逆系統(tǒng)方法的無軸承異步電機(jī)徑向位置解耦控制，真正實(shí)現(xiàn)了無軸承異步電機(jī)徑向兩自由度位置的動(dòng)態(tài)解耦，有效避免了控制過程中由于徑向位移的相互耦合導(dǎo)致的轉(zhuǎn)子徑向振動(dòng)，并對(duì)解耦后的線性子系統(tǒng)進(jìn)行了閉環(huán)設(shè)計(jì)。整個(gè)系統(tǒng)的設(shè)計(jì)在Matlab7. O/Sirnulink平臺(tái)上進(jìn)行了仿真實(shí)現(xiàn)。仿真試驗(yàn)表明了該解耦控制策略的有效性，同時(shí)，設(shè)計(jì)的閉環(huán)控制系統(tǒng)具有良好的動(dòng)、靜態(tài)特性，對(duì)進(jìn)一步的實(shí)驗(yàn)研究具有重要的理論指導(dǎo)意義。