摘    要：多重穩定性是許多分子生物模型重要的動力學行為，它在分析細胞分裂和生長現象中起到關鍵性的作用。為了了解細胞內的復雜的調節網絡的動力學行為，將其數學模型進行單調分解為若干個單調控制系統的互聯。對具有惟一定義的穩定狀態響應的單調控制系統，引入了具有保持局部穩定性質的簡化系統，根據簡化系統的平衡點與原來單調控制系統的平衡點之間存在的一一對應的映射關系，可推知單調控制系統的平衡點的位置及其穩定性，進而通過確定單調控制系統的平衡點的位置及平衡點的穩定性，來確定整個互聯單調控制系統的平衡點的位置及平衡點的穩定性。由于簡化系統降低了原來生物系統模型的雛數，這為分析復雜生物系統的穩定性提供了一種可行的途徑。

關鍵詞：多重穩定性；單調控制系統；簡化系統；平衡點

中圖分類號：TP 27    文獻標識碼：A

    在基因后組時代，生物學家和數學家面臨的****的挑戰就是通過對復雜的細胞內的調節網絡的研究來了解細胞的具體行為。在細胞內，是由蛋白質、DNA，RNA、代謝產物和其他物質組成的調節網絡來處理外部的環境信號、控制內部事件（如基因表達）以及產生適當的細胞響應。尤其支持多重穩定性和周期性行為的調節網絡近年來越來越受到人們的關注：多重穩定性是許多分子生物模型重要的動力學行為，在分析細胞分裂和生長現象中起到關鍵性的作用。多重穩定性及相關的滯后和振蕩現象是分子系統生物研究的重點。

    在應用單調控制系統理淪時所面臨的****的困難就是決定穩定狀態的位置和數量。文獻[3]把復雜的系統分解成由帶有單輸入單輸出的單調系統通過單位反饋連接成具有惟一定義的I/O特性和滿足單調性條件的閉環系統，然后根據簡化定理把單調分解后的閉環系統簡化為一維離散迭代方程。然而文獻[3]，考慮的I/O特性及I/S特性都是單值函數，本文通過把文獻[3]中的結論推廣到I/S及L／O特性是多值函數的情況，介紹能保持原單調系統的局部穩定性質的簡化系統及通過分柝簡化系統的穩定性來推斷原單調系統的穩定性。

  單調動力系統通常是定義在有序巴拿赫空間上的，這里所討論的有序巴拿赫空間是一個實空間B，且具有一個奇異的非空閉子集。在這篇文章里，所討論的K是定義在歐式空間上的，且是一個非空閉凸集。它具有以下幾種性質：

    由上述正錐K的定義，引入序的概念。

    定義1（偏序關系）若x1≥x2，當且僅當x1-X2∈K則稱≥為定義在K上的偏序關系。

    考慮具有輸入輸出的非線性控制系統：

 

    式中，x∈X，u ∈U，y∈y，且x是Rⁿ上的一個開子集的閉包且賦予了由K^X∈R所誘導的序；輸出集Y和輸入集U也分別是其自己內部的閉包且賦予了由錐K^Y∈R和K^U∈R^P所誘導的序。

    在不引起混淆和從文中司以知其意的情況下，可以統一用K來代替K^X，K^Y，K^U。同時，假設：

    f：X×U—y Rⁿ在XxU上是連續可微的且f在x上滿足局部利普希茨條件和在U 上是一致連續的，函數h：X一Y在X上也是連續的。

    下面給出單調控制系統的定義。

    定義2（單調控制系統）  若系統(1)滿足下面給出的條件：

   則稱系統(1)是單調控制泵統。

    x(i，εi，ui)是微分方程x(t)=f(x(t)，u(t))且滿足初始條件x(0)=ε的解。由單調控制系統的定義，還可進一步給出強單調控制系統的定義。

    定義3（強單凋控制系統）  若系統(1)滿足下面給出的條件：

    則稱系統(3)是單調控制系統。

    引理1[3]對系統(1)，V=intX，W= intU都是有序凸集，且f是連續可微的，對于由K^（ε）和K^（δ）所誘導的序，若：

    對所有的i∈ {l，2，…，n}和所有的j∈{l，2，…，m}都成立，則系統(1)是單調系統。其中，

   定義4（I/S特性）考慮系統(1)，若對每一個常量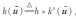輸入u(t)恒等于U，都存在一個全局漸近穩定的平衡點，則稱k(．)：U-V為系統(1)的箭態I/O特性。

    注意到這里k^x是連續非遞減的，即若：

 

    事實上，對任意給定的初始狀態ε和輸入u(t)，v(t)∈U，t≥0，根據單調性的定義，有：

    在分析基因調節網絡模型的多重穩定性時，單調動力系統思想是很重要的一個分析手段。在對一個具體的基因調節網絡模型來說，可以根據一些數學處理方法（如相容性原則）或算法（如LUP算法等），把原來的基因調節網絡模型分解成由單調子系統級聯而成的閉環系統。考慮非線性系統：

    且根據文獻[1]中E．D Sontag所提出的單調分解方法，有：

    定義5（單調分解）  若系統(6)可以分解成下面形式：

    其中，狀態變量X∈X∈Rⁿ；M為控制變量且在U∈R^m取值，而且分別存在由錐K^X∈Rⁿ，K^U∈R^m所誘導的序≤x，≤u，使得：

    ①每一個固定的u，系統(7)都是單凋的。

    ②對每一個固定的x，有u1≤u2，u1≤u2，f（x，u1）≤f（x，u2）成立。

    ③存在一維連續函數h：有x1≤x2，h(x1)≤h(x2)成立。

    ④g(x)=f(x，h(x))

    則稱系統(7)是對系統(6)的一個單調分解。

    引理2對于給定的單調控制系統(6)，若其具有非退化的I/S特性，則x ∈X為系統(7)的一個平衡點當且僅當x∈K^x (h (x))，且映射x一(h(x)，x)是系統(7)的平衡點與對應的滿足x∈k^x(u)，U=K(x)的點(u，x)之問的一個雙射。

    對于引理2中給出的多值函數K^x，可進一步考慮多值函數k：u一P(u,)說若一個系統滿足性質（H）： (H)任意的x1，x2∈E，若x1≠x2，則h(xl)≠h(x2)則稱系統具有性質(H)。 其中，E為系統的平衡點集。

引理3若系統(7)具有性質（H），目具有非退化的I/O特性，則映射x一h（x）是系統(7)的平衡點與對應的滿足u∈K(U)的點H之間的一個雙射。

    證明由引理2可知，若x是系統(7)的一個平衡點，則滿足x∈K^x (h (x))。根據多值函數k的定義有h(k)∈k(h(k))。反過來，若u∈k(u)則存在X∈K^x (u)，使得h(x)=u，因此x∈K^x (h (x))由引理2可知，x是系統的一個平衡點。

    如果假設：u一x是單值函數且滿足上述定理的條件，即有以下的定理：

    定理1若系統(7)具有性質(H)，且礦是單值函數，滿足：

    ①具有非退化的I/S特性和I/O特性。

    ②其閉環系統(6)是強單調系統。

    ③其解有界。

    局部漸近穩定平衡點與系統(7)的局部漸近平衡點之間的一個雙射，且系統(7)的幾乎所有有界解都收斂于其漸近穩定平衡點。

    證明若u是系統u= k(u) 的一個平衡點，則u是方程u=k(u)=h(K^x (u))的一個解：顯然有：

    因此系統(7)的一個平衡點。反過來，若x是系統(7)的一個平衡點，則對應的輸出力y=h(x)，又由于u=y可得x= K^x（y），因此：

    于是y是系統u=k(u)-u的一個平衡點。

    L／S特性K^x是可微函數，事實上，由K^x (u)是方程，f（K^x(u),u）=O的解和非退化的假設知，對任意的u，f(x,u)=0對x的偏微分都是可逆的，根據隱含映射定理知K^x是可微的。而且還可以通過對方程f（K^x （u），u）=O兩邊求導：

  進而可得：

  這里，A，B，C定義為

  且由I／S特性k^x是非退化的假設知，A^-1存在：

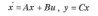    考慮單位反饋u=y，得閉環系統z=(A+BC)z，由于A是Hurwtz矩陣，且det（I+CA^-1B）≠O。由文獻[4]的定理2知矩陣-（I+CA^-1B）是Hurwtz矩陣，且存在Perron-Frobenius特征值u，若u

    在上述的定理中，系統u=k( u)-u 稱之為連續時間簡化系統，它保持了原系統(6)的局部穩定性質。在具體分析生物系統的多重穩定時，由于簡化系統降低了原生物系統的維數，其維數等于其輸入的維數：這在分析生物系統的穩定時提供了方便。下面就以一個實例來說明簡化系統在分析生物系統穩定性時所表現出的簡便性。

4實例

    為了說明文中的主要結果，考察一類真核單細胞有機體（如酵母菌）的基因調節網絡：在文獻[9]中，Iiskhaikow在研究中發現這些生物體能產生一種蛋白質，且這種蛋白質能穿過細胞膜去促進信使RNA的生成。不僅如此，在細胞內部發現另一種蛋白質也能影H向信使RNA的轉錄，記其濃度為λ。讓r，p，q分別表示信使RNA、內部蛋白質、外部蛋白質的濃度，則基因調節網絡可以用以下的閉環系統模型來描述：

(s)系統的關聯圖，如圖l所示。

   

    在這里，函數H，T滿足，偏導H與偏導P的比值大于0，偏導H與偏導a的比值大于0．且T(r)>0，H，T分別為轉錄速和翻譯速率。a1，a2，a3為降解系數，常量k1，k2分別為蛋白質通過細胞膜進來和出去的速率。為了研究閉環系統(8)的穩定性，根據文獻L4]所提出的單調分解方法，可以把原閉環系統(8)看成是由開環系統(9)通過單位反饋u=h(p，q，r)聯接而成的。

    命題l系統(9)具有性質（H）。

    證明假設(p1，q1，r1)，(p2，q2，r2)是系統(9)的2個平衡點，若：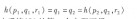

    則由系統(8)的第一個方程可得P1=p2，進而可得r1=r2。所以系統滿足性質（H）。

    由引理1可知系統(9)為單調控制系統，且根據試驗數據可以得出系統(9)具有惟一定義的單值函數k，即對每一個固定的輸入u都存在惟一的平衡狀態與之對應。令：

    由式(10)可得：

    顯然，q(u)就是所討論的I／O特性K。為了便于下面的討論，給出函數H，T的一般形式：

    由上述的定理可知，系統(9)的局部漸近穩定平衡點與簡化系統u=u(k)-u的局部漸近穩定平衡點是一一對應的.令q(u)=u，取m=4，n=1，ki=l／6，ke =l／l5，al=1，a2=l／10，a3=1／6，A1=l，A2=1，A4=10，BI=16，B2=10：其仿真圖，如圖2所示。

 

5結語

    多重穩定性是許多分子生物模型重要的動力學行為，它在分析細胞分裂和生長現象中起到關鍵性的作用。本文對具有惟一定義的穩定狀態響應的單調控制系統，為了確定單調控制系統的平衡點的位置及平衡點的穩定性引入了保持局部穩定性質的簡化系統。簡化系統保持了原系統的局部穩定性質，由于簡化系統降低了原生物系統的維數，其維數等于其輸入“的維數。這在分析生物系統的穩定時提供了方便。