摘    要：針對一類含有輸入時變時滯的結構振動系統，研究了在執行器發生故障情況下系統全局漸近穩定的魯棒甘。可靠控制設計的問題、首先根據建筑結構力學原理，建立了包含控制輸入滯后、執行器故障等的結構系統狀態模型。然后基于Lyapunov穩定性理論和線性矩陣不等式處理方法給出了一個時滯依賴型H_∞；可靠主動控制算法，且控制器存在的充分條件以線性矩陣不等式的形式給出：通過對一個四自由度建筑結構模型在EI Centro地震波作用下振動的主動控制仿真，驗證了所提方法的可行性，可用于工程結構的振動控制。

關鍵詞：結構振動系統；H_∞器錯控制；輸入時變時滯；時滯依賴；執行器失效

中圖分類號：TP 273    文獻標識碼：A

    近年來，隨著抗震工程及防災減災事業的發展，結構系統的主動控制已成為土木工程領域的研究熱點，國內外學者提出了諸如****控制、模態控制、神經網絡控制及模糊控制等多種控制算法，并取得了優異的成績。文獻[2]對結構系統的H_∞性進行了研究，但沒有對其他性能進行研究；文獻[3]不僅在保證系統具有H。性能的基礎上還對結構參數的攝動具有一定的魯棒性；文獻[4]在上述性能的基礎上還對執行器增益飽和問題進行了初步的研究。然而這些方法主要研究了結構系統的減震性和對參數攝動的魯棒性，而對結構系統的輸入滯后和可靠性問題的分析仍很缺乏，但對這類問題的研究很縣有工程實用意義。其中，輸入時滯效應已成為一個不容忽視的問題，盡管多數情況下這種時滯很小，但仍會使作動器作動規則與系統不同步而導致被控系統失穩，文獻[5-6]研究了輸入滯后的問題，但沒有考慮其他性能分析問題；另外，可靠控制也是控制系統能夠正常運行的關鍵因素之一，在涉及生命安全的實際工程應用中結構控制系統的可靠性顯得尤為重要，但可靠控制在該領域的應用尚未見報道。

    針對上述問題，在文獻[7母]的基礎上推出一個可滿足多約束條件可靠控制器的設計方法，可同時解決振動工程領域所遇到的上述實際問題。

    考慮如下n自由度的結構系統：

式中，M，C，K分別為系統的質量矩陣、阻尼矩陣和剛度矩陣；Bu,Bw0，分別為輸人參數矩陣和外部干擾參數矩陣；φl(t)為系統的初始位移，且連續二階光滑可導。

    假設輸入時滯d(t)滿足O≤d(f)≤r且0≤d(t)≤d

式中，x(t)∈Rn為系統狀態變量；U(t-d(t))∈Rn為系統的實際控制輸入；系統初始值φ(t)為連續光滑的向量函數由式(1)得到，且：

    被調輸出設為

式中，C為調整系統性能的權值矩陣；調節．D可以限制控制器增益。

    針對系統(2)，本文取狀態反饋控制律為

  

    考慮到執行器可能失效，本文采用執行器開關型故障模型，引入故障開關矩陣L，并將其放在矩陣B和反饋控制陣K之間，其形式為

    其中，Ω為執行器故障開關中各種可能故障的集合。

3主要結果

  考慮存在執行器失效情況，不確定時滯系統在控制器(3)作用下，有下列故障閉環系統：

    注意式(5)需要區間[-2τ，0]上的初始條件，當Vt<-τ時x(t)=O。

    對于輸入時滯系統的魯棒可靠鎮定性問題，有如下主要結論。

    定理1對于不確定線性時滯系統(1)，如果存在矩陣置，正定矩陣P，Q，S>O，S≤P^-l使得如下LMI不等式成立：

存在一個魯棒可靠控制器，且在其作用下，系統(4)是具有H范數有界。

    證明首先證明矩陣不等式(6)可保證閉環系統(5)魯棒鎮定性，具體如下：

    由O

    定義Lyapunov函數為

可得Lyapunov函數沿方程(5)解軌跡的導數為

    從上面的推到過程可以看出，當不考慮干擾，式(7)中隱含不等式即V(x(t)，0) <0，根據Lyapunov穩定性定理，系統(5)是一致漸近穩定的，所以閉環系統(4)也是一致漸近穩定的。因為式(7)考慮了執行器失效的情況，所以閉環系統(4)也是魯棒可靠鎮定的。

  其次，證明矩陣不等式(7)是保證閉環系統式(4)在零初始條件下具有日。范數的有界。

  假設初態x(t)=0，并引進函數：

    注意到由于故障閉環系統的魯棒穩定性保證了||z(t) ||：有界性和limx(t)=O，在零初始條件下，對任意w(o)∈L2[0，∞]，有以下不等式成立：

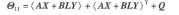
則存在狀態反饋控制器u(t一d(t)) =Kx(t一d(t))使得故障閉環系統(4)是魯棒H_∞可靠控制系統，且控制器增益為K= YX^-1。

    證明用對角矩陣分別左乘和右乘式(6)，并利用Schur補引理可得到等價的線性矩陣不等式(10)，其中，X=P^-1，y= KX，Q =xQx，S與X滿足S≤X，證畢。

4仿真算例

    選取一個4自由度的結構模型作為研究對象，其振動模型的原始參數參考了文獻[4]。系統的振動方程由式(1)給出，系數矩陣為

   綜上所述，給定正常數y>0，對于任意執行器失效情況L∈Ω，若存在對稱正定矩陣P，Q，S及矩陣K使得式(6)成立，則受干擾的故障閉環系統(4)是魯棒日。可靠控制系統，且控制器增益為k。至此，定理1得證。

    不等式(6)不是線性矩陣不等式，為了便于數值計算，以下通過定理2將其轉化為線性矩陣不等式( LMI)。

    定理2考慮具有時變輸入時滯的不確定系統(4)，給定正常數7>0，對于任意執行器失效情況￡tn，若存在對稱正定矩陣x，Q，S和矩陣Y，且滿足s -x≤0使得下面矩陣不等式成立：

w(t)為El Centro( NS，1940)地震波加速度x0(t)，峰值為0 34 g，采樣周期為0.02 s，選取振動最激烈的前10 s進行仿真。下面仿真中d均取0.1。

  首先，考慮執行器任意失效情況下，對****輸入滯后Tmax與干擾抑制度y之間的關系進行了仿真研究。在取定不同的v值并結合定理2和LMI工具箱可以得到不同的****時滯值點，將其連成曲線，如圖1所示。

   

    由于抑制度y值越小表示結構系統對地震波的抑制能力就越強，因此從圖中可以看出結構系統可容許的****輸入滯后值隨著對地震波抑制能力的增大而減小。該結果在工程選擇硬件設備時很具有指導意義，特別是片機的運算速度、傳感器反應時間和執行器的響應時間等。

  然后，輸入滯后T取15 ms，7取0 5，且考慮執行器任意一個失效情況下通過對定理2進行求解得到控制器增益矩陣：

  下面單獨檢驗系統的可靠性（無輸入滯后）。將所求代人式(4)，得到在執行器各種失效的情況下地震波加速度到結構頂層加速度的頻率響應曲線。在執行器失效及在普通（不考慮容錯的）控制器。作用下的頻率響應曲線，如圖2所示。

 

   

    從圖2(a)可看出，在任一執行器失效結構頂層****加速度在不同頻率地震波作用下具有很好的增益抑制能力，說明該控制的可靠性較強。圖2(b)與圖2(a)比較，可明顯發現普通日。控制算法在有執行器失效時對地震的抑制能力較差，不具有容錯性能。本文控制器設計方法；將在涉及生命安全的實際振動工程應用中起到較大的改善作用。綜合驗證該系統在具有時變輸入滯后情況下且有執行器失效時是否仍可以滿足所需性能要求。利用S．muimk軟件搭建模塊，其中，控制輸入滯后取15 ms，控制律K不變，仿真得到結構頂層的控制效果，如圖3所示。

   

    圖3中1為無控（即不加控制）、2為執行器失效、3為全控（執行器都正常）。曲線1與曲線3同時比較，位移反應平均抑制百分之60，加速度反應平均抑制百分之45，說明控制器在容許范圍內可存在輸入滯后且進一步說明該控制器有容錯能力。

5  結  語   

  本文針對結構振動控制中常見問題，如控制輸入滯后、執行器失效、控制器增益飽和，結合現代控制理論中的魯棒日。容錯控制算法提出一種控制器設計方法，并通過仿真實例驗證該方法具有較強

的應用性，電為土木結構的振動控制提供了一種安全可靠且較有工程實用意義的研究方法。另外，利 用本文所得到的輸入時滯與干擾抑制間的關系，在實際工程中選擇硬件時將起到很好的指導作用。

  為進一步對結構振動系統的應用性研究，在滿足上述控制性能要求的基礎上，對結構系統對結構 參數攝動的魯棒性以及結構系統的非線性等問題進行了較深入的研究，有關內容將另文介紹。