劉元江 洪南生 陳世坤(西安交通大學7100409)
【摘 要】針對圓筒型籠式直線感應電動機的特點,通過建立回路方程,求解電機的瞬態特性,計算結果與實驗結果基本吻合。
1引 言
目前,圓筒型直線感應電動機廣泛應用在往復運動的機構中。由于它的初級是開放磁路,并且次級磁路不具有對稱的特點,使得其瞬態特性很難分析,直接用“場”的方法求解,計算工作量較大,費時較多。用傳統的“每相”等效電路的方法求解,誤差較大。例如,不能較準確地計及邊端效應的影響,并且“每相”的等效電路模型只適合于分析正弦穩態。
本文針對圓筒型籠式直線感應電動機磁路的特點,建立了d—q模型,在d、q坐標系下,建立電壓平衡方程。為了考慮縱向邊端效應,增加次級的計算極數,延拓次級的計算范圍。利用建立的模型,分析電機的瞬態推力特性、瞬態電流特性和瞬態速度特性。
2電機的基本結構
所研究的圓筒型直線感應電動機的軸向剖面圖如圖1所示。初級齒部由硅鋼片疊壓而成,軛部由鋼管做成,槽中嵌以餅式線圈。次級為車有環形槽的鋼元,槽中鑲嵌了銅環。當初級繞組中通人三相電流時,如果固定次級,初級就會朝某一方向作直線運動。試制樣機的數據為:
電壓=220v,頻率=50hz,相數=3,極數=6,初級鐵心長=o.185m,初級外徑=0.130m,初級極距=0.03m,初級槽數=18,次級槽距=o.009m。
3模型的建立
基于以下假設建立模型:
(1) 初、次級鐵心的導磁率無限大,即忽略鐵心磁阻。
(2)初、次級鐵心的電導率σ=o,即忽略鐵心損耗。
(3)初、次級鐵心的表面光滑,以卡氏系數修正氣隙。
(4)次級籠式繞組等效為導電薄板,放在次級表面,等效的原則是兩者的每極銅截面積相等。
3.1電壓方程的建立
建立d-q坐標系,將d-q坐標系固定在初級上,并且q軸與初級a相繞組的軸線一致。通過式(1)進行坐標變換,將初級每相的電壓、電流、磁鏈變換到d—q坐標系中。
矩陣中f代表電壓、電流、磁鏈。
為了計及縱向邊端效應,初級鐵心和次級在縱向的出端增加兩極,在入端增加一極,對于本樣機,可建立20個電壓回路平衡方程式。
電壓方程式按式
列出,以uds,ur1為例:
式中 uds,udr1——初級d軸電壓和次級第一個極的d軸電壓
rs,rrl——初級每相電阻和次級第一個極的電阻
ids,idr1——初級c,軸電流和次級第一個極的d軸電流
λds,λdr1——初級d軸交鏈的磁鏈和次級第一個極的d軸交鏈的磁鏈
eds,edrl——初級d軸速度電壓和次級第一個極的d軸速度電壓將所有的電壓方程寫成矩陣形式為:
式中 [u]——電壓矩陣,[u]=[udsuqs,0, 0,…o]t
[i]——電流矩陣,[i]=[ids,iqs,idr1,iqr1,…iqr9]t
[r]——電阻矩陣,[r]=diag[rs,rs,r1,r2…r9]t
[l]——電感矩陣,[l]=[lm]+[lδ]
[lm]——主電感矩陣
[lδ]——漏電感矩陣
v x——電機的運行速度矩陣[l]、 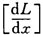 中的主電感元素及其對位移的微分,分別由下兩式計算: 式中 l12——繞組1、2間的互感,如n1(x)
=n2(x),則為自感
n1(x),n2(x)——繞組函數
d2——初級外徑
gc——有效氣隙
l——初級鐵心的計算長度矩陣[lδ]的元素按文獻2的方法計算。
3.2計算繞組函數
只考慮繞組函數的基波分量,將繞組函數的諧波分量用漏電感計,則初級三相繞組的繞組函數為:
式中ns——每槽的匝數
通過變換式
求得初級d軸和q軸的繞組函數nds,nqs。
次級每一極的d軸和q軸的繞組函數按文獻3的方法求得,例如第一個d軸、q軸繞組函數的表達式為:
3.3電磁力和速度的計算
為了分析電機的運行狀態,建立相應的機械系統運動方程:
式中 v0——初級的初始速度,在合閘起動瞬時,它等于零
a——加速度
f——電機運動過程中的摩擦力
m——質量
fc——軸向電磁力
設在時間△t內,加速度為常數,則式(3)變為:
4計算與分析
利用建立的模型,對實驗樣機加185v的電壓,結合初始條件,[i]t=0=0,用四階龍格庫塔法求解式(2),得出電流,再利用式(5)、(6)求取推力、速度。計算曲線分別如圖2、圖3、圖4所示。
由于受實驗條件的限制,只測了三相瞬態電流,如圖5所示。為了進一步驗證方法的
正確性,我們還用此方法求出了平均速度以及s=1.o時的起動推力和起動電流。計算結果和實驗結果如附表所示。
從實測的結果和計算的結果可看出,瞬態電流的****值與穩態值之比為1.45,比普通的旋轉電機要小,并且瞬態過程較快。在電機進入穩態后,三相電流的幅值不同,說明三相電流不平衡,這是因為電機初次級繞組和磁路不對稱。在整個運動過程中,推力曲線中除含有基頻脈振的力波外,還包含有雙倍基頻脈振的力波,速度基本上隨時間線性增加。
5結論
本文利用d—q模型分析了圓筒型籠式直線電動機的瞬態特性。所建立的模型簡單易行,并且能計及直線感應電動機特有的邊端效應,計算結果與實驗結果基本吻合。用此模型求解所需的計算機內存少,所用的時間遠遠小于用“場”的方法求解所用的時間。
進入:
劉元江 洪南生 陳世坤(西安交通大學7100409)
【摘 要】針對圓筒型籠式直線感應電動機的特點,通過建立回路方程,求解電機的瞬態特性,計算結果與實驗結果基本吻合。
1引 言
目前,圓筒型直線感應電動機廣泛應用在往復運動的機構中。由于它的初級是開放磁路,并且次級磁路不具有對稱的特點,使得其瞬態特性很難分析,直接用“場”的方法求解,計算工作量較大,費時較多。用傳統的“每相”等效電路的方法求解,誤差較大。例如,不能較準確地計及邊端效應的影響,并且“每相”的等效電路模型只適合于分析正弦穩態。
本文針對圓筒型籠式直線感應電動機磁路的特點,建立了d—q模型,在d、q坐標系下,建立電壓平衡方程。為了考慮縱向邊端效應,增加次級的計算極數,延拓次級的計算范圍。利用建立的模型,分析電機的瞬態推力特性、瞬態電流特性和瞬態速度特性。
2電機的基本結構
所研究的圓筒型直線感應電動機的軸向剖面圖如圖1所示。初級齒部由硅鋼片疊壓而成,軛部由鋼管做成,槽中嵌以餅式線圈。次級為車有環形槽的鋼元,槽中鑲嵌了銅環。當初級繞組中通人三相電流時,如果固定次級,初級就會朝某一方向作直線運動。試制樣機的數據為:
電壓=220v,頻率=50hz,相數=3,極數=6,初級鐵心長=o.185m,初級外徑=0.130m,初級極距=0.03m,初級槽數=18,次級槽距=o.009m。
3模型的建立
基于以下假設建立模型:
(1) 初、次級鐵心的導磁率無限大,即忽略鐵心磁阻。
(2)初、次級鐵心的電導率σ=o,即忽略鐵心損耗。
(3)初、次級鐵心的表面光滑,以卡氏系數修正氣隙。
(4)次級籠式繞組等效為導電薄板,放在次級表面,等效的原則是兩者的每極銅截面積相等。
3.1電壓方程的建立
建立d-q坐標系,將d-q坐標系固定在初級上,并且q軸與初級a相繞組的軸線一致。通過式(1)進行坐標變換,將初級每相的電壓、電流、磁鏈變換到d—q坐標系中。
矩陣中f代表電壓、電流、磁鏈。
為了計及縱向邊端效應,初級鐵心和次級在縱向的出端增加兩極,在入端增加一極,對于本樣機,可建立20個電壓回路平衡方程式。
電壓方程式按式
列出,以uds,ur1為例:
式中 uds,udr1——初級d軸電壓和次級第一個極的d軸電壓
rs,rrl——初級每相電阻和次級第一個極的電阻
ids,idr1——初級c,軸電流和次級第一個極的d軸電流
λds,λdr1——初級d軸交鏈的磁鏈和次級第一個極的d軸交鏈的磁鏈
eds,edrl——初級d軸速度電壓和次級第一個極的d軸速度電壓將所有的電壓方程寫成矩陣形式為:
式中 [u]——電壓矩陣,[u]=[udsuqs,0, 0,…o]t
[i]——電流矩陣,[i]=[ids,iqs,idr1,iqr1,…iqr9]t
[r]——電阻矩陣,[r]=diag[rs,rs,r1,r2…r9]t
[l]——電感矩陣,[l]=[lm]+[lδ]
[lm]——主電感矩陣
[lδ]——漏電感矩陣
v x——電機的運行速度矩陣[l]、 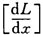 中的主電感元素及其對位移的微分,分別由下兩式計算: 式中 l12——繞組1、2間的互感,如n1(x)
=n2(x),則為自感
n1(x),n2(x)——繞組函數
d2——初級外徑
gc——有效氣隙
l——初級鐵心的計算長度矩陣[lδ]的元素按文獻2的方法計算。
3.2計算繞組函數
只考慮繞組函數的基波分量,將繞組函數的諧波分量用漏電感計,則初級三相繞組的繞組函數為:
式中ns——每槽的匝數
通過變換式
求得初級d軸和q軸的繞組函數nds,nqs。
次級每一極的d軸和q軸的繞組函數按文獻3的方法求得,例如第一個d軸、q軸繞組函數的表達式為:
3.3電磁力和速度的計算
為了分析電機的運行狀態,建立相應的機械系統運動方程:
式中 v0——初級的初始速度,在合閘起動瞬時,它等于零
a——加速度
f——電機運動過程中的摩擦力
m——質量
fc——軸向電磁力
設在時間△t內,加速度為常數,則式(3)變為:
4計算與分析
利用建立的模型,對實驗樣機加185v的電壓,結合初始條件,[i]t=0=0,用四階龍格庫塔法求解式(2),得出電流,再利用式(5)、(6)求取推力、速度。計算曲線分別如圖2、圖3、圖4所示。
由于受實驗條件的限制,只測了三相瞬態電流,如圖5所示。為了進一步驗證方法的
正確性,我們還用此方法求出了平均速度以及s=1.o時的起動推力和起動電流。計算結果和實驗結果如附表所示。
從實測的結果和計算的結果可看出,瞬態電流的****值與穩態值之比為1.45,比普通的旋轉電機要小,并且瞬態過程較快。在電機進入穩態后,三相電流的幅值不同,說明三相電流不平衡,這是因為電機初次級繞組和磁路不對稱。在整個運動過程中,推力曲線中除含有基頻脈振的力波外,還包含有雙倍基頻脈振的力波,速度基本上隨時間線性增加。
5結論
本文利用d—q模型分析了圓筒型籠式直線電動機的瞬態特性。所建立的模型簡單易行,并且能計及直線感應電動機特有的邊端效應,計算結果與實驗結果基本吻合。用此模型求解所需的計算機內存少,所用的時間遠遠小于用“場”的方法求解所用的時間。
|