交流電動機轉子槽漏磁導數(shù)值積分計算

    董超奎  (西安微電機研究所)

    【摘  要】本文提出一種交流電動機轉子槽下部漏磁導的數(shù)值積分計算方法。與傳統(tǒng)的漏磁導算法相比，這種方法省去了推導漏磁導計算公式的繁瑣過程，而直接從磁導概念出發(fā)，利用數(shù)值積分計算給出漏磁導數(shù)值。文中提出的方法對電機漏磁導的計算具有普遍意義。

    【敘  詞】交流電動機，轉子，槽，漏磁，磁導，數(shù)值積分，計算

引 言

    交流電動機轉子通常采用的槽形有梨形槽、梯形槽及多級梯形槽。對于前兩類槽形的槽下部漏磁導計算，習慣上常用查曲線的方法。對于后一類槽形，即多級梯形槽，其槽下部漏磁導的計算多采用公式與曲線相結合的方法。用手算時這種方法頗為繁瑣；在用計算機計算編程時需要把曲線擬合成公式。

    本文提出一種利用數(shù)值積分計算多級梯形槽下部漏磁導的方法。這種方法從漏磁導概念出發(fā)，不用推導出漏磁導的具體計算公式，可方便、正確地實現(xiàn)槽下部漏磁導的計算。

  1數(shù)學模型及計算原理

    本文所討論的轉子多級梯形槽如圖l所示。計算槽漏磁導時，假設

    a．電流在槽內均勻分布；

    b．忽略鐵心磁壓降．即認為鐵的磁導率為無窮大；

    c．槽中所有磁力線平行于槽口。根據(jù)槽漏磁導的概念可知

式中  λ_L—槽下部漏磁導；

    Z—整個槽內所含導體數(shù)；

    z_x一高度x處至槽底所含導體數(shù)；

    2y—高度x處槽的寬度。

    積分沿槽高進行(不包括槽口高h_R。)

    對于轉子槽，z_x與Z之比可轉化為它們所對應的面積之比，因此有

式中 As—槽總面積(不含槽口面積h_Ro b_Ro)；

    As—高度x處至槽底面積。

    由此可見，λ_L的計算實質上是一個積分的計算，如能找出Ax 2y與x之關系，則沿槽高求積分，即可求出λ_L之值。

    通常，f(x)是一個比較復雜的函數(shù)，這樣再對f(x)求積分將更加復雜。特別是對于圖l所示的多級梯形槽，這種積分運算將相當復雜、繁鎖。由于計算機具有速度快、精度高的特點，適合于數(shù)值計算，因此可采用數(shù)值積分法來計算式(2)的積分值。

1．1 As的數(shù)學模型

    A_s為槽的總面積，即為槽中三部分梯形面積之和，則有

1．2 A_x，2y的數(shù)學模型

1．Zl槽底梯形

由圖2可得

1．2．2槽中間梯形

由圖3可得

將式(13)，(14)代入上式，化簡，并經(jīng)變量替換，可得

1．Z3槽斜肩梯形

    從圖4可見

    將式(17)，(18)代入上式，經(jīng)化簡，積分變量替換后可得

2漏磁導的計算

將以上導出的

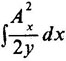表達式代入式(2)，即可求出λ_L。如前所述，只要將積分算出，計算λ_L的問題即可解決。這里，采用數(shù)值積分法計算以上各個積分，進而計算出漏磁導λ_L。

3程序框圖

在以上分析基礎上編制計算機程序。As的計算比較簡單，可以直接寫出。分析s1、S2和S3表達式可知，它們的積分表達式是相似的，因此可用一個函數(shù)子程序來表示，調用時用實際參數(shù)代替虛擬參數(shù)即可。積分使用具有快速收斂性及高精度的Rombeng積分法，并把其編制成一個子程序，供計算S1、s2及S3時調用。整個程序框圖如圖5所示。

4源程序

用FORTRAN77語言編制轉子槽下部漏磁導的計算程序，經(jīng)實例計算表明，程序是正確、可靠的，該程序稍作修改即可作為一子程序，進行電機優(yōu)化設計、性能校核等程序中使用。

對于實際中常用的轉子槽形，如刀形槽(圖6)、凸形槽(圖7)、半凸形槽，梯形槽及瓶形槽，都可用此模型及程序計算其槽下部漏磁導，只要給有關變量賦以適當值即可。例如：當k_R1=b_Ro，h_R0=k_R1=0時，為刀形槽；當b_R2=b_R1時，為凸形槽及半凸形槽；當h_R3=0，b_R3=b_R4=b_R2時，為梯形槽；當h_R1=h_R3b_R1=b_R0=b_R3=b_R4=bR₂時，為瓶形槽。

5結  語

本文給出了用數(shù)值積分計算轉子槽下部漏磁導的方法。該方法的特點是

a．直接從漏磁導的概念出發(fā)，采用數(shù)值積分方法計算漏磁導，避免了推導和使用復雜的公式。

  b．概念清晰，計算程序簡單。

  c．適合于任何槽形的槽漏磁導計算，因此，對槽漏磁導的計算具有普遍意義。

參考文獻

1上海電器科學研究所．中小型三相異步電動機電磁計算程序。197 1